heureka

Circle gamma intersects the hyperbola y=1/x  at (1,1), (3, 1/3) and two other points. What is the product of the y coordinates of the other two points?

\(\ldots\)continue

\(\begin{array}{rcll} \boxed{ y^4-y^3\left(6x_0-\frac{32}{3}\right)+y^2\left(8x_0-\frac{38}{3}\right)-y\cdot2x_0+1= 0} & (1)\\ \end{array} \)

\(\text{We have two roots $y_1 = 1$ and $y_2 = \dfrac{1}{3}$, } \\ \text{So formula $(1)$ can be written as}: \)

\(\begin{array}{|rcll|} \hline && (y-y_1)(y-y_2)(y-y_3)(y-y_4) \quad | \quad y_1 = 1 \qquad y_2 = \dfrac{1}{3} \\ &=& (y-1)\left(y-\dfrac{1}{3}\right)(y-y_3)(y-y_4) \\ &=& (y^2-\dfrac13y - y+\dfrac13 )(y^2-yy_4-yy_3+y_3y_4 ) \\ &=& \left(y^2-\dfrac43y +\dfrac13 \right) \left(y^2-y(y_3+y_4)+y_3y_4 \right) \\ && \ldots \\ &=& y^4-y^3\left(\dfrac43 +y_3+y_4 \right) + y^2 \left( y_3y_4-\dfrac43(y_3+y_4 + \dfrac13 \right) - y \left(\dfrac43 y_3y_4-\dfrac13(y_3+y_4) \right) + \dfrac13y_3y_4 \\ \hline \end{array}\)

Compare:

\(\small{ \begin{array}{|rclclclclcl|} \hline && y^4 &-&y^3\left(6x_0-\frac{32}{3}\right) &+&y^2\left(8x_0-\frac{38}{3}\right) &-&y\cdot2x_0 &+& \color{red}1 \\ &=& y^4 &-&y^3\left(\dfrac43 +y_3+y_4 \right) &+&y^2 \left( y_3y_4-\dfrac43(y_3+y_4 + \dfrac13 \right) &-& y \left(\dfrac43 y_3y_4-\dfrac13(y_3+y_4) \right) &+& \color{red}\dfrac13y_3y_4 \\ \hline \end{array} } \)

\(\text{So $ 1 = \dfrac13 y_3y_4 \Rightarrow y_3y_4 = 3$} \)

The product of the y coordinates of the other two points is 3

1. Let $r(\theta) = \frac{1}{1-\theta}$. What is $r(r(r(r(r(r(30))))))$ (where $r$ is applied $6$ times)?

\(\begin{array}{|rcll|} \hline r(\theta) &=& \dfrac{1}{1-\theta} \\ \hline r(r(\theta)) &=& \dfrac{1}{1-\dfrac{1}{1-\theta}} \\\\ &=& \dfrac{1-\theta}{1-\theta-1 } \\\\ &=& \dfrac{1-\theta}{ -\theta } \\\\ &=& \dfrac{\theta-1}{ \theta } = 1-\dfrac{1}{\theta} \\\\ \hline r(r(r(\theta))) &=& \dfrac{1}{1- (1-\dfrac{1}{\theta}) } \\\\ &=& \dfrac{1}{1- 1 + \dfrac{1}{\theta} }\\\\ &=& \dfrac{1}{ \dfrac{1}{\theta} } \\\\ &=& \theta \\ \hline r(r(r(r(\theta)))) &=& \dfrac{1}{1-\theta} \\ \hline \end{array}\)

This is a cycle:

\(\begin{array}{|r|r|c|} \hline \text{cycle} & & \ldots r(r(\theta) \\ \hline 1 & \text{once} & \color{red}\dfrac{1}{1-\theta} \\ \hline 1 & \text{twice} & \color{green}\dfrac{\theta-1}{ \theta } \\ \hline 1 & 3\text{ times} & \color{blue}\theta \\ \hline\hline 2 & 4\text{ times} & \color{red}\dfrac{1}{1-\theta} \\ \hline 2 & 5\text{ times} & \color{green}\dfrac{\theta-1}{ \theta } \\ \hline 2 & 6\text{ times} & \color{blue}\theta \\ \hline \ldots & \ldots& \ldots \\ \hline \end{array} \)

\(\text{So $r(r(r(r(r(r(\theta)))))) = \theta $ and $ r(r(r(r(r(r(30)))))) = \mathbf{30} $ } \)

2. If $f(a) = \frac{1}{1-a}$, find the product $f^{-1}(a) \times a \times f(a)$. (Assume $a \neq 0$ and $a \neq 1$.)

\(\begin{array}{|rcll|} \hline f{\color{red}(}f^{-1}(a){\color{red})} &=& a \\\\ f {\color{red}\Big(}\dfrac{a-1}{a}{\color{red}\Big)} &=& a \quad & | \quad \text{see table above } r\left(\dfrac{\theta-1}{\theta} \right) = \theta \\\\ \text{so } \\\\ f^{-1}(a) &=& \dfrac{a-1}{a} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline && f^{-1}(a) \times a \times f(a) \\\\ &=& \dfrac{a-1}{a}\times a \times \dfrac{1}{1-a} \\\\ &=& \dfrac{a-1}{1-a} \\\\ &=& -\dfrac{1-a}{1-a} \\\\ &=& -1 \\ \hline \end{array}\)

Circle gamma intersects the hyperbola y=1/x  at (1,1), (3, 1/3) and two other points.

What is the product of the y coordinates of the other two points?

\(\text{Let $P_1 = (x_1 = 1,\ y_1 = 1)$} \\ \text{Let $P_2 = (x_2 = 3,\ y_2 = \frac13 )$} \\ \text{Center of the circle $= (x_0,\ y_0)$} \\ \text{Radius of the circle $= r $} \)

Formula of the circle:

\(\begin{array}{|lrcll|} \hline & (x-x_0)^2+(y-y_0)^2 &=& r^2 \\ \hline P_1(x_1,y_1): & (x_1 - x_0)^2 + (y_1 - y_0)^2 &=& r^2 \\ P_2(x_2,y_2): & (x_2 - x_0)^2 + (y_2 - y_0)^2 &=& r^2 \\ \hline (1)=(2): & (x_1 - x_0)^2 + (y_1 - y_0)^2 &=& (x_2 - x_0)^2 + (y_2 - y_0)^2 \\ & \Rightarrow \\ & ax_0+by_0 &=& c \\ & y_0 &=&\dfrac{c-ax_0}{b} \\ & &=& 3x_0-\dfrac{16}{3} \\ & \boxed{a=2(x_2-x_1) = 4 } \\ & \boxed{b=2(y_2-y_1) = -\dfrac{4}{3} } \\ & \boxed{c=x_2^2 +y_2^2-x_1^2-y_1^2=\dfrac{64}{9} } \\ \hline \end{array} \)

Circle intersects the hyperbola \(y=\dfrac{1}{x} \text{ or } x=\dfrac{1}{y}\)

\(\begin{array}{rcll} (x-x_0)^2+(y-y_0)^2 &=& r^2 \quad & | \quad r^2 = (x_1-x_0)^2+(y_1-y_0)^2 \\ (x-x_0)^2+(y-y_0)^2 &=& (x_1-x_0)^2+(y_1-y_0)^2 \quad & | \quad x=\dfrac{1}{y} \\ \left(\dfrac{1}{y}-x_0 \right)^2+(y-y_0)^2 &=& (x_1-x_0)^2+(y_1-y_0)^2 \\ \Rightarrow \\ \end{array} \\ \begin{array}{rcll} \boxed{ y^4-y^3\left(6x_0-\frac{32}{3}\right)+y^2\left(8x_0-\frac{38}{3}\right)-y\cdot2x_0+1= 0} \\ \end{array} \)

Examples calculated by WolframAlpha:

\(\begin{array}{|l|l|lr|l|} \hline x_0 & y_0 & y_3 & y_4 & y_3\cdot y_4 \\ \hline 1.4226 & -\dfrac{3.1966}{3} & -1.75493 & -1.70947 & 3.00000\ldots \\ 1.2 & -\dfrac{5.2}{3} & -4.06132 & -0.738675 & 2.99999\ldots \\ 1 & -\dfrac{7}{3} & -3-\sqrt{6} & \sqrt{6}-3 & 3 \\ 0.5 & -\dfrac{11.5}{3} & -8.65331 & -0.346688 & 2.99999\ldots \\ \hline \end{array} \)
 

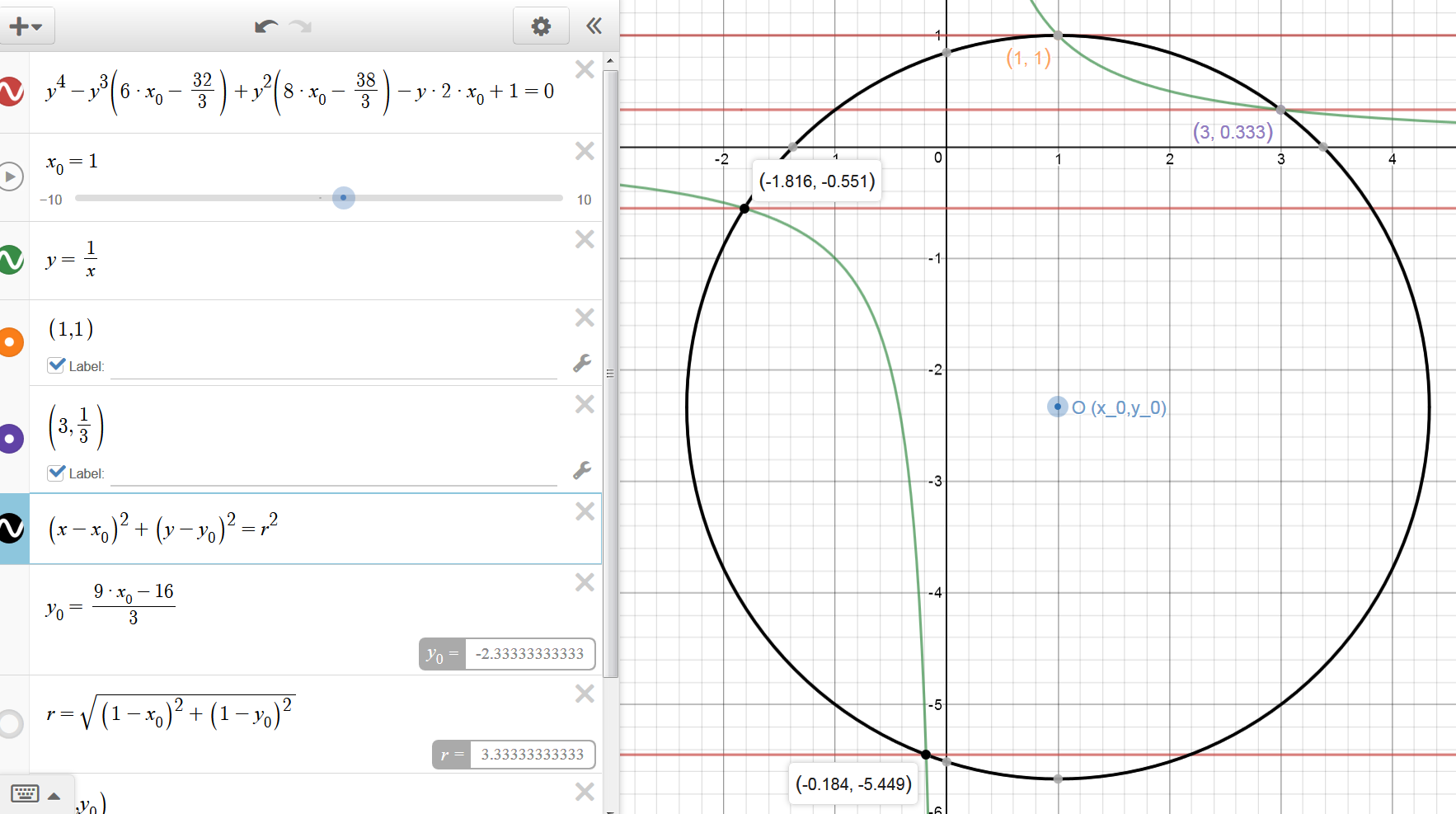
I assume theproduct of the y coordinates of the other two points is 3

Suppose that x,y,z are positive integers satisfying x≤y≤z, and such that the product of all three numbers is twice their sum. What is the sum of all possible values of z?

sum of z is 4+5+8 = 17

the question says that

p>q>0

find the length of the line segment joining these pairs of points.

(p , q) and (q , p)

these are the coordinates. 

\(\begin{array}{|rcll|} \hline \text{length} &=& \sqrt{(p-q)^2+(q-p)^2} \\ &=& \sqrt{(p-q)^2+\Big(-(p-q)\Big)^2 } \\ &=& \sqrt{(p-q)^2+\Big( (-1)(p-q) \Big)^2 } \\ &=& \sqrt{(p-q)^2+(-1)^2(p-q)^2 } \quad & | \quad (-1)^2 = 1^2 = 1 \\ &=& \sqrt{(p-q)^2+1\cdot(p-q)^2 } \\ &=& \sqrt{(p-q)^2+(p-q)^2 } \\ &=& \sqrt{2\cdot (p-q)^2 } \\ &\mathbf{=}& \mathbf{(p-q)\sqrt{2}} \\ \hline \end{array}\)

Finding distance using absolute values?

b)

\(\text{Let $x$ is the kilometre marker at the end } \\ \text{Because the markers become big in the direction of east $x$ is greater than $3$ km }:\)

\(\begin{array}{|r|r|r|r|} \hline \text{part} & \text{from marker} & \text{to marker} & \text{distance} \\ \hline 1 & 2\ \text{km} & 7\ \text{km} & 7-2 = 5\ \text{km} \\ \hline 2 & 7\ \text{km} & 3\ \text{km} & 7-3 = 4\ \text{km} \\ \hline 3 & 3\ \text{km} & x\ \text{km} & x-3 \ \text{km} \\ \hline & & & \text{sum} = 15\ \text{km} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline 5 + 4 + x-3 &=& 15 \\ 9+x-3 &=& 15 \\ 6+x &=& 15 \\ x &=& 15 - 6 \\ \mathbf{x}& \mathbf{=}& \mathbf{9\ \text{km}} \\ \hline \end{array}\)

At the end of the scanvenger hunt Toby is at the 9-km marker.

a)

\(\begin{array}{|r|r|r|r|} \hline \text{part} & \text{from marker} & \text{to marker} & \text{distance} \\ \hline 1 & 2\ \text{km} & 7\ \text{km} & 7-2 = 5\ \text{km} \\ \hline 2 & 7\ \text{km} & 3\ \text{km} & 7-3 = 4\ \text{km} \\ \hline 3 & 3\ \text{km} & 9\ \text{km} & 9-3 = 6\ \text{km} \\ \hline \end{array}\)

In the last interval Toby travel 6 km.

A vertical pole is 15 ft high and the length of its shadow is 20 ft.

What is the angle of elevation of the sun rounded to the nearest tenth of a degree? 

\(\begin{array}{|rcll|} \hline \tan(\text{elevation}) &=& \dfrac{15\ \text{ft.} }{20\ \text{ft.} } \\\\ &=& \dfrac{3}{4} \\\\ &=& 0.75 \\\\ \text{elevation} &=& \arctan(0.75 ) \\ &=& 36.8698976458^{\circ} \\ &=& 36.9^{\circ} \\ \hline \end{array}\)

1. Let $f(x) = Ax - 2B^2$ and $g(x) = Bx$, where $B \neq 0$. If $f(g(1)) = 0$, what is $A$ in terms of $B$?
2. Suppose that $f$ is a function and $f^{-1}$ is the inverse of $f$. If $f(1)=2$, $f(2) = 6$, and $f(3)=5$, then what is $f^{-1}(f^{-1}(6))$?

\(\begin{array}{|r|r|r|r|} \hline x & f(x) \\ \hline 1 & 2 & f(1) = 2 & f^{-1}(2) = 1 \\ 2 & 6 & f(2) = 6 & f^{-1}(6) = 2 \\ 3 & 5 & f(3) = 5 & f^{-1}(5) = 3 \\ \hline f^{-1}(x) & x \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline f^{-1}(6) &=& 2 \\ f^{-1}(f^{-1}(6)) &=& f^{-1}(2) \\ &=& 1 \\\\ \mathbf{f^{-1}(f^{-1}(6))}& \mathbf{=}& \mathbf{1} \\ \hline \end{array}\)

1. Let $f(x) = Ax - 2B^2$ and $g(x) = Bx$, where $B \neq 0$. If $f(g(1)) = 0$, what is $A$ in terms of $B$?
2. Suppose that $f$ is a function and $f^{-1}$ is the inverse of $f$. If $f(1)=2$, $f(2) = 6$, and $f(3)=5$, then what is $f^{-1}(f^{-1}(6))$?

\(\begin{array}{|r|r|r|r|} \hline x & f(x) \\ \hline 1 & 2 & f(1) = 2 & f^{-1}(2) = 1 \\ 2 & 6 & f(2) = 6 & f^{-1}(6) = 2 \\ 3 & 5 & f(3) = 5 & f^{-1}(5) = 3 \\ \hline f^{-1}(x) & x \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline f^{-1}(6) &=& 2 \\ f^{-1}(f^{-1}(6)) &=& f^{-1}(2) \\ &=& 1 \\\\ \mathbf{f^{-1}(f^{-1}(6))}& \mathbf{=}& \mathbf{1} \\ \hline \end{array}\)

1. Let $f(x) = Ax - 2B^2$ and $g(x) = Bx$, where $B \neq 0$. If $f(g(1)) = 0$, what is $A$ in terms of $B$?

2. Suppose that $f$ is a function and $f^{-1}$ is the inverse of $f$. If $f(1)=2$, $f(2) = 6$, and $f(3)=5$, then what is $f^{-1}(f^{-1}(6))$?

\(\begin{array}{|lrcll|} \hline x = 1 : & g(x) &=& g(1) \\ & g(1) &=& B\cdot 1 \\ & g(1) &=& B \\\\ & f(g(1)) &=& f(B) \\ x=B: & f(B) &=& A\cdot B - 2B^2 \\ f(B) = 0: & A\cdot B - 2B^2 &=& 0 \\ & A\cdot B&=& 2B^2 \\ & A &=& \dfrac{2B^2}{B} \quad & | \quad B \ne 0~ ! \\ &\mathbf{ A }& \mathbf{=}& \mathbf{ 2B } \\ \hline \end{array} \)