September 6, 2020:
Happy Sunday everybody! (or whatever day of the week it is…)
Before we start, there was this really (and I do mean really) interesting question that caught my eye: https://web2.0calc.com/questions/please-help_95143
I checked it out...and guess what? I could not find an answer!
I’m not sure whether it was me that understood the problem wrong or not. There was a guest that already answered the question, but I’m not sure if their interpretation is right or not…
Anyways, I would like to congratulate all the answerers that contributed today:
- Doggo
- Dragan
- hulu0104
- asinus
- Omi67
- Alan
- Melody
- jugoslav
- joliel3
I have not had as much enthusiasm and motivation to answer as last week...who knows why? Maybe because I aged a year...but I hope to find that motivation sometime soon…
News:
There is not much news for today, except for something Melody has noticed.
She told me that the forum was much “livelier” (if that is the correct word) in the past than it is now.
Back then, each post would turn into something to joke about (that actually is true, I read some old posts, and WOW, boy were they much “livelier” than today’s).
The newer members are very intelligent, and are learning a lot, but the “liveliness” has gone down a bit.
Since she (Melody) has been such an important role in the forum, I think there is a way to make this forum a bit “livelier” (boy have I used that word A LOT).
And that is….A CONTINUED FORUM THREAD THINGY.
WHAT!?????
I know. Even I have no idea what I am talking about. But, I was thinking, that maybe because of all that couch potatoing that we have been doing for the past….who knows how long….we have lost our motivation and excitement.
So, I will be starting a “continued forum thread thingy” tomorrow. Everyone can participate, and yes, it is math related.
So here is how it works. The topic is “2012” math competitions (because that is when the calculator was created). You can search up an archive of 2012 math competitions, from AMCs to AIMEs to MathCounts.
I will start with a question. Then someone answers and posts a new question. Then someone answers that question and posts a new question...and so on. So that is one thing to look forward to tomorrow.
The next four days are going to be busy, as there will be many math competitions, continued forum thingies, and much more. Here is what I hope the schedule would look like:
Monday: 2012 Math Competition continued thread thingy
Tuesday: Answer Competition (as tuesday is international literacy day. More will be explained in tomorrow’s post)
Wednesday: Sudoku Competition (Wednesday is international sudoku day)
Thursday: Remainder Game (more would be explained on wednesday’s wrap)
Answering Tip:
Beware of the pronouns. Don’t use the word, “it” too much, as some people might not know what “it” defines. Let me give you an example of an imaginary answer that uses “it” too much:
Is it a fraction or not? 3x + 4 = 12 is what we want to solve. It has two terms, 3x and 4. It equals to 12. We subtract 4 from it and that is 8. We divide it by 3, and we get it’s answer, which is 8/3. So we know that it is a fraction.
Though this question is relatively easy, you still can follow along. But, we see that the word “it” has been used to describe 5 different things. We also never told what “it” is. Based on “it has two terms”, we might think that “it” describes the left side of the equation, but that is after a long period of thought. But then, “it” is used to describe 12, and then “it” is used to describe 8.
That is it for tonight!
Stay tuned for the next four days, as it would be filled with lots of “math fun”. It would be weird if nobody joined…
- ilorty
September 5, 2020:
I can’t believe it is already the 5th!
I would like to introduce to you a pet of mine, the headlesschicken.
He follows me around, and if I ever get annoyed at a user, he is the account I will use to calm myself down. So, if you ever find him anywhere, (he is always getting lost), stay calm, even though he might be an ugly sight.
Anyways, here are the members that have answered with proper answers:
- asinus
- Alan
- jugoslav
- Dragan
- joliel3
You might have noticed, I have never put my name in there, whether I answered or not. It would be weird if I did though...and not so modest. headlesschicken reminded me that modesty is very important, so he erased my name off the answerers list.
How to submit an answer:
Okay, everybody should know how to submit an answer...right?
Yes, that is true, but some answers are a pain to look at! (okay, maybe not a pain, but it could be better ;P )
Let me ask you a question. Would you rather look at an answer that is like this:
We know that x is = to y so we can say that 2x = 2y. From here, we also see that x > 78 and y is less than 80. This will tell us that 2x is equal to 2y is useless, and therefore we must not use it for any case. After some math we see that the only integer solution is x and y = 79 because that is what the inequalities tell us. And that is the end of my answer hope it helps u please give like and have a nice day.
Or would you like to see an answer like this:
To begin this question, we see that x is equal to y.
x = y
To find the integer value of x and y, we need some guidelines. Using the information that we know, we can say:
x > 78
y < 80
In other words:
78 < x, y < 80
This means that we need to find the number that is between 78 and 80. We see that there is only one number, and that is 79. Therefore, x and y are equal to 79.
Obviously, we would like the second one much better, right? I know that it takes WAY longer to write that, but trust me, you don’t need to lift your bottom off that couch or change out of those pjs that you have been wearing for three days in a row.
So starting from now, each wrap (maybe not forever) will have a writing tip for you to better structure your answer.
Here is today’s tip: Give your equations their own line. It makes it SO much easier to read, and it looks much more organized.
Problem of the day:
Though this is a math forum, there have not been questions that make you go: AHA! I know what to do now!
So, to sharpen everyone’s “logic” skills, I have brought to you a question for you to solve.
2014 AIME Problem 8
The positive integers N and N2 both end in the same sequence of four digits abcd when written in base 10, where digit a is not zero. Find the three-digit number abc.
This problem CAN be done with guess and checking, BUT, there is a mathematical way to do it, because the answer is actually quite BIG. DO NOT POST THE ANSWER AS A REPLY TO THIS THREAD.
Bug news:
There have been quite a few bugs lately, some that you might have noticed, some that might have slipped through.
There was one bug that was fixed very recently. Before, you could not press the down arrow on the leaderboard or the watchlist unless you were on the main page. Now, you can!
And….that wraps up the wrap!
- ilorty
September 4, 2020:
To all those who had suffered the tragedy of my wrong links: I have corrected them! And, I would like to say why those led to nowhere. Many people who HAVE included links have had them lead to nowhere, even though the link address is right...this problem will be covered later.
First, I would like to thank these members for answering questions with real proper answers (that were not copied, or don’t have an explanation, and were not based off of guess and checking) today (the order does not mean anything):
- Nacirema
- asinus
- jugoslav
- Alan
- Omi67
- heureka
- Melody
And...those are all the answerers that answered after 8PM GMT. If I missed you, I am terribly sorry. I made sure to check the answer tab, so your name might have not been on there because the answer was not “proper”.
Continuing on…
How to make a link that does not lead to 404 Page Not Found:
There have been a lot of links recently that have led to 404 Page Not Found, including some of mine.
The links are correct, it is just that there is a space ( ) after the link. The program cannot detect if that space is part of the link or not, so it will just assume that that space is a character, which changes the link.
Make sure that you do not add any extra “spaces” after the link to ensure that it leads to the right place.
News:
Most of the bugs have been fixed, including the LaTeX bug that did not render LaTeX. For members, this is now fixed, but when I logged on as a guest just to check if LaTeX worked, it did not render. (or it may just be me)
The "giving likes" bug is also fixed, so give as many likes to your answerers as you want!
There is still another bug that I will elaborate on in the “Bugs” section.
Bugs:
There is this one bug that happens when you post multiple times in a row. Sometimes you are able to post multiple times in a row without this picture showing up:
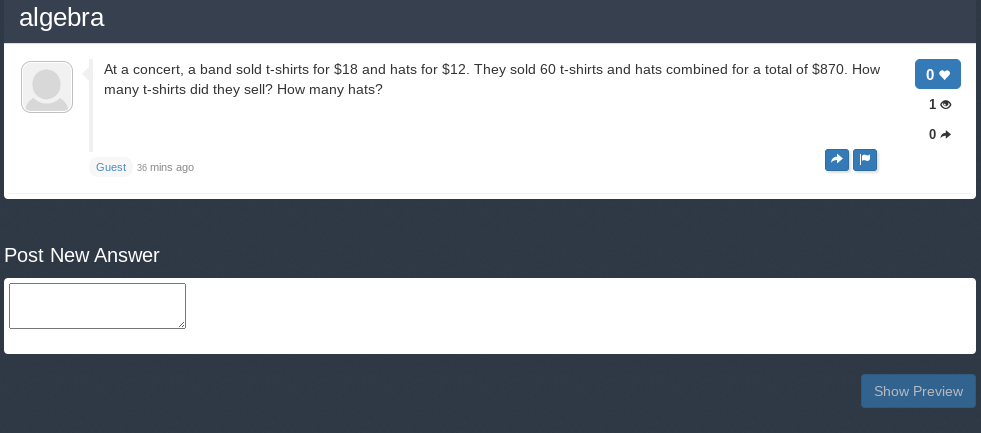
(This picture was taken by gwen)
I have addressed this problem here:https://web2.0calc.com/questions/glitch-on-site-or-is-it-only-me
If you are facing the issue, you can head over to that link.
How to upload a picture for Safari/Chrome users:
I promised to make a guide for uploading pictures on today’s wrap, and so I did. There have been lot’s of guides, but none of them work on Safari or Google Chrome, so I will tell you how I get my pictures.
1. Go to imgur.com
2. Press “New Post”
3. Press “Choose Photo or Video”
4. Select the photo you want
5. Once the photo is successfully uploaded, use a mouse and LEFT CLICK the image (for mobile devices, long click the image)
6. Select “Open image in new tab”
7. Go to the new tab, and copy the link
8. Head over to web2.0calc.com and create your post
9. Press the “image” button and paste the link you copied
Voila! Your image should be ready. Remember to RESIZE it, just to make sure that it is not too big. (go to first wrap to see how to resize)
I’m sorry I was not able to upload the images. The file was too big to download...but hopefully the instructions are easy to follow.
That is it for tonight!
- ilorty
Lantern Thread: https://web2.0calc.com/questions/lantern-thread-september-2-9