The only part of the function that has the ability to restrict the domain is the denominator; the numerator plays no role in this. For this reason, we should only focus on the denominator and ignore the numerator.
Our job, in this case, is to determine the smallest value of c that will forever prevent a divisor by zero. Let's try and do that.
| \(x^2+4x+c=0\) | By setting the denominator equal to zero, we will see what solutions result in a real input that equals zero. Let's use the quadratic formula. |
| \(a=1,b=4,c=c;\\ x_{1,2}=\frac{-4\pm\sqrt{\textcolor{red}{4^2-4*1*c}}}{2*1}\) | We want to focus on the discriminant because that determines whether or not there are real solutions for a given quadratic. |
| \(16-4c<0\) | When the discriminant is less than zero, there are no real solutions. This means that there will no input that causes a domain restriction. |
| \(16<4c\) | |
| \(4 < c\text{ or }c > 4\) | The immediate integer after 4 is 5, so this is the smallest integer that will result in no domain restriction. |
| \(c=5\) | |
| \(c(\textcolor{red}{a},\textcolor{blue}{b},\textcolor{green}{c})= \frac{\textcolor{red}{a}}{\textcolor{blue}{b}}+ \frac{\textcolor{blue}{b}}{\textcolor{green}{c}}+ \frac{\textcolor{green}{c}}{\textcolor{red}{a}};\\ c(\textcolor{red}{2},\textcolor{blue}{12},\textcolor{green}{9})= \frac{\textcolor{red}{2}}{\textcolor{blue}{12}}+ \frac{\textcolor{blue}{12}}{\textcolor{green}{9}}+ \frac{\textcolor{green}{9}}{\textcolor{red}{2}}\) | This shows the relationship of the input to the problem at hand. It is now necessary to convert all fractions to common denominators so that we can simplify the right-hand side. The LCM, in this case, is 36. |
| \(c(a,b,c)=\frac{6}{36}+\frac{48}{36}+\frac{162}{36}\) | |
| \(c(a,b,c)=\frac{216}{36}=6\) | That's quite a nice result, don't you think? |
Problems like these can be daunting, but it is important to perservere and be observant. I was unsure of the solution, so I decided to attempt to find the solution by drawing 0 straight lines to 5 straight lines. I have created an image of my final solutions to all of these. The red line on each indicates where I added a line from the previous image.
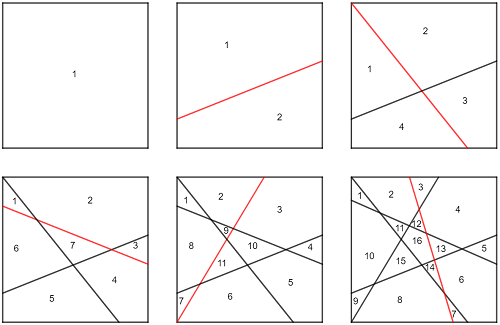
I will the notation \(f(n)\) to notate the maximum number of regions generated with n straight lines. I could not go much further than this, so I decided to stop here.
\(f(0)=1\\ f(1)=2\\ f(2)=4\\ f(3)=7\\ f(4)=11\\ f(5)=16\\ \)
I immediately noticed a pattern with this sequence of numbers. This is what I noticed
\(f(0)+1=f(1)\\ f(1)+2=f(2)\\ f(2)+3=f(3)\\ f(3)+4=f(4)\\ f(4)+5=f(5)\)
This is a quadratic relationship since the numbers 1,2,3,4, and 5 have a second common difference of 1. This means that there is a quadratic equation out there that represents this exact situation. Let's try and find it, shall we? Let's start this by plugging in that \(f(0)=1\):
| \(f(n)=an^2+bn+c\) | Since we already determined that the above relationship can be observed quadratically, let's plug in some values to develop that quadratic. |
| \(f(0)=1;\\ f(0)=a*0^2+b*0+c\) | This is the easiest one to simplify. |
| \(\boxed{1}\hspace{3mm}1=c\) | We now know that the constant term of the quadratic is 1. |
Let's plug in the next point, \(f(1)=2\):
| \(f(1)=2;\\ f(1)=a*1^2+b*1+c\) | Now, simplify both sides completely. |
| \(2=a+b+c\) | We established in \(\boxed{1}\) that \(c=1\), so let's substitute that in here. |
| \(2=a+b+1\) | Substract 1 from both sides. |
| \(\boxed{2}\hspace{3mm}1=a+b\) |
Let's plug in the next point, \(f(2)=4\):
| \(f(2)=4;\\ f(2)=a*2^2+b*2+c\) | Simplify from here. |
| \(4=4a+2b+c\) | As aforementioned, \(c=1\), so substitute this information in and simplify completely. |
| \(4=4a+2b+1\) | Subtract 1 from both sides again. |
| \(\boxed{3}\hspace{3mm}3=4a+2b\) | |
Our next task is to solve this system of equations. Let's do that. I will solve by substitution here because of the presence of a variable with a coefficient of one.
\(\boxed{2}\hspace{3mm}1=a+b\Rightarrow a=1-b\)
Since I have a isolated, it is possible to substitute it in for \(\boxed{3}\):
| \(\boxed{2}\hspace{3mm}a=1-b;\\ \boxed{3}\hspace{3mm}3=4(1-b)+2b\) | Solve for b in \(\boxed{3}\). |
| \(3=4-4b+2b\) | |
| \(-1=-2b\) | |
| \(b=\frac{1}{2}\) | Let's substitute this into \(\boxed{2}\). |
| \(b=\frac{1}{2};\\ \boxed{2}\hspace{3mm}a=1-\frac{1}{2}\) | |
| \(a=\frac{1}{2}\) | All the variables have been solved for now! |
After all this work, we have determined that \(f(n)=\frac{1}{2}n^2+\frac{1}{2}n+1\) is the quadratic that represents the maximum number of regions for n straight lines. In this case, n=15, so let's substitute this in and solve.
| \(n=15;\\ f(15)=\frac{1}{2}*15^2+\frac{1}{2}*15+1\) | Simplify the right hand side of the equation. |
| \(f(15)=\frac{225}{2}+\frac{15}{2}+\frac{2}{2}\) | Now, do the addition. |
| \(f(15)=\frac{242}{2}=121\text{ regions}\) | You're done! |
Arithmetic sequences are written in the form of the following:
\(a_n=a_1+d(n-1)\).
an is the nth term of the sequence
a1 is the first term of the sequence
d is the common difference
n is the desired term number
1) We already know the information necessary to write an equation for the nth term of this sequence.
| \(a_1=-7; d=\frac{5}{2}\\ a_n=-7+\frac{5}{2}(n-1)\) | The only thing left to do is simplify. Distributing is the first step to accomplish this. |
| \(a_n=-\frac{14}{2}+\frac{5}{2}n-\frac{5}{2}\) | Combine like terms. |
| \(a_n=\frac{5}{2}n-\frac{19}{2}\) | This is completely simplified. |
2) There is a formula that exists for the summation of an arithmetic series or geometric series, but that probably would not help your understanding anyway; I can derive it for you, though.
We have to know the last term, and we can generate this by using the formula from before: \(a_n=a_1+d(n-1)\). Therefore, n=10, d=5, and a1=5:
| \(a_{10}=-5+5(10-1)\) | Evaluate this to determine the last term of the sequence. |
| \(a_{10}=-5+5*9\) | Simplify the right hand side. |
| \(a_{10}=40\) | |
Now, let's attempt to evaluate the sum. Standard notation dictates \(S_n\) for the summation.
| \(S_{10}=-5+0+...+35+40\\ S_{10}=\hspace{2mm}40+35+...+0\hspace{2mm}-5\\ \overline{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\\ 2S_{10}=\underbrace{35+35+...+35+35}=35*10=350\\ \hspace{24mm}\text{10 times}\\ S_{10}=175\) | All I did here is reverse the same sum and added both of them together. This made it significantly easier to determine the sum. |
I did not answer every question here because the others can be answered with the knowledge given above, albeit not directly. Try and figure it out yourself.
One way to approach this problem is to find the area of the circle and subtract the area of the minor sector and the area of the three congruent triangles.
Let's find the area of the circle:
| \(A_{\circ}=\pi*6^2\) | Use the formula for the area of a circle. |
| \(A_{\circ}=36\pi\text{ft}^2\) | |
Let's find the area of the minor sector:
| \(A_{\text{sector}}=\frac{1}{4}A_{\circ}\) | This minor sector is really just a quarter of the area of the entire circle. |
| \(A_{\text{sector}}=\frac{1}{4}*36\pi\text{ft}^2\) | |
| \(A_{\text{sector}}=9\pi\text{ft}^2\) | |
Let's find the area of the three congruent triangles that are right and isosceles:
| \(A_{\triangle}=\frac{1}{2}*6*6\) | It is not too difficult to find the area of these triangles since they are all right. |
| \(A_{\triangle}=18\text{ft}^2\) | |
| \(3A_{\triangle}=3*18\text{ft}^2\) | Thus far, I have calculated the area of one triangle, but we need to calculate the area of all three. |
| \(3A_{\triangle}=54\text{ft}^2\) |
Now that we know everything, let's find the area of the three minor segments of this particular circle:
| \(A_{\text{segments}}=A_{\circ}-A_{\text{sector}}-3A_{\triangle}\) | Do the substitution. |
| \(A_{\text{segments}}=(36\pi-9\pi-54)\text{ft}^2\) | Combine like terms. |
| \(A_{\text{segments}}=(27\pi-54)\text{ft}^2\) | Match this with the answer choices above. |
Solving for a variable can be extremely daunting--especially in a multivariable equation such as \(5x^2-x=8y^2+\frac{9xy}{4}\). I have a few suggestions that may make this easier to do.
1. Move everything to One Side of the Equation.
This is a relatively simple step.
\(5x^2-x=8y^2+\frac{9xy}{4}\Rightarrow8y^2+\frac{9x}{4}y-5x^2+x=0\)
2. Eliminate All Instances of Fractions or Decimals
Fractions can be pesky, and there is no reason to make a hard situation worse. In this case, we can multiply both sides of the equation by 4 to eliminate the fractions. In a situation like this one, this is also relatively easy to do.
\(8y^2+\frac{9x}{4}y-5x^2+x=0\Rightarrow32y^2+9xy-20x^2+4x=0\)
3. Use a Formula to Finish it Off
This is written in the form of a quadratic, so the quadratic formula is the way to go.
| \(a=32; b=9x;c=-20x^2+4x\\ y_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\) | The only thing left to do is plug in the numbers. |
| \(y_{1,2}=\frac{-9x\pm\sqrt{(9x)^2-4*32(-20x^2+4x)}}{2*32}\) | It is time to simplify. |
| \(y_{1,2}=\frac{-9x\pm\sqrt{81x^2-128(-20x^2+4x)}}{64}\) | |
| \(y_{1,2}=\frac{-9x\pm\sqrt{81x^2+2560x^2-512x}}{64}\) | |
| \(y_{1,2}=\frac{-9x\pm\sqrt{2641x^2-512x}}{64}\) | I have now successfully solve for y. |
Both of these questions have been recently asked before, so I will redirect you to pages where others have already answered these questions because I see no reason to duplicate answers.
Question #1: https://web2.0calc.com/questions/if-abcde-x-4-edcba-what-is-the-number-abcde-as-usual
Question #2: https://web2.0calc.com/questions/steven-bakes-brownies
Cphill gets credit for the second question.
DanielCai, obviously your answer of 10.5 cannot be right since \(a<0\). I would evaluate \(g(g(g(10.5)))\) one step at a time.
| \(g(x) = \left\{ \begin{array}{cl} -x & x\le 0, \\ 2x-41 & x>0. \end{array} \right.\) | This is the function's definition. Now, let's evaluate \(g(10.5)\) |
| \(g(10.5)=2\cdot 10.5-41\\ \hspace{13mm}=21-41\\ \hspace{13mm}=-20\) | Since \(10.5>0\), evaluate the bottom function. |
| \(g(-20)=-(-20)\\ \hspace{13mm}=20\) | Since \(-20\leq0\), evaluate the top function. |
| \(g(20)=2\cdot 20-41\\ \hspace{10mm}=40-41\\ \hspace{10mm}=-1\) | Since \(20>0\), evaluate the bottom function. |
Now, let's do the same process with \(g(g(g(a)))\).
| \(g(x) = \left\{ \begin{array}{cl} -x & x\le 0, \\ 2x-41 & x>0. \end{array} \right.\) | This is the function definition. | ||
| \(g(a)=-a\) | Since \(a\leq0\) was a set parameter given at the beginning of the problem, | ||
| \(g(-a)=-2a-41\) | Since multiplying a by -1 would make \(-a>0\), so evaluate it as the bottom fraction. | ||
| I do not know if \(-2a-41>0\), so I have to consider both cases. | ||
Set these two cases equal to -1 and check both solutions.
| \(2a+41=-1\) | \(-4a-123=-1\) |
| \(2a=-42\) | \(-4a=122\) |
| \(a=-21\) | \(a=-\frac{122}{4}=-\frac{61}{2}\) |
When checking both solutions, only \(a=-\frac{61}{2}\) works.