CPhill

$90

9 tens

1 twenty and 7 tens

2 twenties  and 5 tens

3 twenties ans 3 tens

4 twenties and 1 ten

(m + n + p)(mn + mp + np)  = 25

m^2n + mn^2 + mnp + m^2p + mnp + mp^2 + mnp+ n^2p + np^2  = 25

[m^2(n + p) +   n^2(m + p) + p^2(m + n)]  + 3(mnp)  = 25

4 + 3mnp  = 25

3mnp =21

mnp  = 7

Well....since it looks as though we're all at the same picnic.....here's my attempt at a weak answer

x^400 = 9^1000

Take the GCF of 400, 1000  = 200  ....so we can write

(x^2)^200 = (9^5)^200        take the 200th root of both sides

(x^2) = 9^5      and we can write

(x^2) = (3^2)^5

x^2  = 3^10      take both roots

x = ± √[3^10]  =   ± [ 3] ^(10/2)  =  ± [3]^5  =  ± 243

THX, Nirvana!!!

2.       We have the following moves  (R R R R  D D D D D D)

So in the set....we can choose any 4 of the 10 positions for the R's to occupy  or, alternatively, any 6 of the 10 positions for the D's to occupy

So....the nuber of possible paths  =  10C 4  = 10C6  =  210 possible paths

Hectictar and I agree.....that might be dangerous...... the Sign of the Apocalypse.!!!

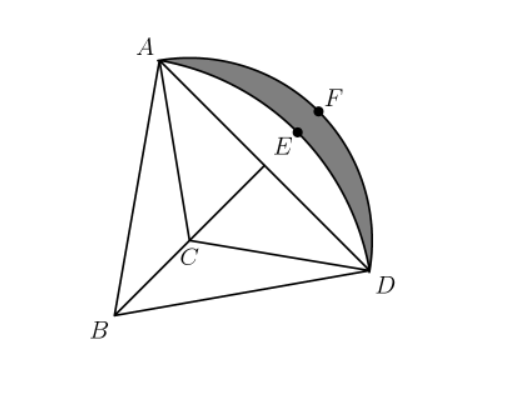
It appears that the chord AD is bisected by  BE

So angle BED is right   and ED  =  1/2 AD  =  10

And we can find angle EBD using the Law of Sines

sin BED          sin (EBD)

_______  =  __________

  BD                 ED 

sin 90              sinEBD

______  =       ______

  20                     10

sinEBD  = (10/20) sin 90

sin EBD  = (1/2) (1)

sin EBD  = 1/2

So....EBD must be  30° 

So.....by symmetry....angle ABD  must be twice this  = 60°  

So....now....we can compute the area of sector AEBD =

pi* BD^2(60/360)  = pi*  (20)^2 (1/6)  = pi * 400/6  = 200/3 pi  units^2

And since angle ACD is twice angle ABD.....then   (1/2)ACD = ABD  =  60° = angle ECD

Then....since DEC is right, then triangle ECD is a 30-60-90 right triangle

Then  

CD / sin DEC  =   ED / sin ECD

CD / 1  =  10/  [sqrt(3)/2 ]

CD  =  20 /sqrt (3)

And the area of sector   AFDC =

pi (CD^2) (120/360)  = pi * (400/3)(1/3)  = (400/9) pi units^2      (1)

Now....we need to caclculate the area of triangle ABD

(1/2)(AB)(BD) sin (60°)   =

(1/2)(20)(20)sqrt (3)/2)  =  100sqrt(3) units^2

So.....the area between chord AD and arc AED  =

Area of  AEBD  - area of triangle ABD  =

  ( [200/3] pi  - 100sqrt(3)  )    (2)  

Lastly....we need to calculate the area of triangle ACD  [note CD = AC ]  =

(1/2)(CD)(AC)sin(120°)  =  (1/2)(20/sqrt3)^2 sqrt(3)/2  =   (1/2)(400/3)sqrt(3)/2 = 100/sqrt(3) = 100sqrt(3)/3   (3)

So....the area we are looking for is : 

Area of sector AFDC  - area between chord AD and arc AED  - area of triangle ACD  =

(1)   - (2)  - (3)  =

[400/9] pi  - [ 200/3 ]pi + 100sqrt(3) - 100sqrt(3)/3=

[ 400/9]pi - [600/9]pi  + (2/3)100sqrt(3)  =

(2/3)100sqrt(3) - (200/9)pi  ≈  45.66 units^2  =  46 units^2

[If I didn't make any errors....LOL!!!  ]

Good job, Guest!!!

I think we'll  take your word for it!!!

LOL!!!!

The number of possible arrangements of the digits  is 4!  = 24

Let's look at those which form even numbers.....this occurs when the "2"  appears at the end of a number

So....in that case.....the other digits can be arranged in 3!  =  6 ways

So.....there are 6 even numbers and 18 odd

So

18 / 24  =   3 / 4     and you are correct!!!!

I believe that there are many such three integer patterns.....for example.... 

64, 176,178   [sum = 418, all are < 180   and all are unique ]

or

66, 174, 178  

A computer program could probably  be designed to generate all the possibilities