heureka

Ich habe diese Frage als Hausaufgabe bekommen und weiss nicht wie ich sie angehen soll?
Um das Becken eines Schwimmbades zu füllen, hat man drei Wasserhähne zur Verfügung.
Jeder Hahn ist verschieden stark. Und daher schneller oder weniger.
Wenn nur Hahn A und Hahn B offen sind dauert es 70 Minuten beziehungsweise 1 Sunde und 10 Minuten.
Wenn nur Hahn A und Hahn C offen sind dauert es 50 Minuten.
Wenn nur Hahn B und Hahn C offen sind dauert es 56 Minuten.
Wie lange dauert es bis das Becken voll ist wenn man alle Hähne aufdreht?

\(\text{Hahn A: $~\dfrac{1}{A}$ in der Einheit $\left[ \dfrac{\text{Becken}} {\text{Min.}} \right] $ } \\ \text{Hahn B: $~\dfrac{1}{B}$ in der Einheit $\left[ \dfrac{\text{Becken}}{\text{Min.}} \right] $ } \\ \text{Hahn C: $~\dfrac{1}{C}$ in der Einheit $\left[ \dfrac{\text{Becken}}{\text{Min.}} \right] $ }\)

\(\small{ \begin{array}{|lrcll|} \hline (1) & \dfrac{1}{A} + \dfrac{1}{B} &=& \dfrac{1~\text{Becken}} {70~ \text{Min.}} \\ (2) & \dfrac{1}{A} + \dfrac{1}{C} &=& \dfrac{1~\text{Becken}} {50~ \text{Min.}} \\ (3) & \dfrac{1}{B} + \dfrac{1}{C} &=& \dfrac{1~\text{Becken}} {56~ \text{Min.}} \\ \hline (1)+(2)+(3): & \dfrac{1}{A} + \dfrac{1}{B} +\dfrac{1}{A} + \dfrac{1}{C} + \dfrac{1}{B} + \dfrac{1}{C} &=& \dfrac{1~\text{Becken}} {70~ \text{Min.}} +\dfrac{1~\text{Becken}} {50~ \text{Min.}}++\dfrac{1~\text{Becken}} {56~ \text{Min.}} \\\\ & 2\cdot \left( \dfrac{1}{A} + \dfrac{1}{B} + \dfrac{1}{C} \right) &=& \left( \dfrac{1} {70} +\dfrac{1} {50}+\dfrac{1} {56} \right) \dfrac{1~\text{Becken}} {\text{Min.}} \\\\ & 2\cdot \left( \dfrac{1}{A} + \dfrac{1}{B} + \dfrac{1}{C} \right) &=& 0.05214285714 \dfrac{1~\text{Becken}} {\text{Min.}} \\\\ & \dfrac{1}{A} + \dfrac{1}{B} + \dfrac{1}{C} &=& 0.02607142857 \dfrac{1~\text{Becken}} {\text{Min.}} \\\\ & \mathbf{\dfrac{1}{A} + \dfrac{1}{B} + \dfrac{1}{C}} & \mathbf{=} & \mathbf{ \dfrac{1~\text{Becken}} {38.3561643836~\text{Min.}} } \\ \hline \end{array} }\)

\(\text{Wenn man alle Hähne aufdreht werden, dauert es $38.3561643836~\text{Min.}\\$oder $ \mathbf{38~\text{Min.}~ 21.4~ \text{Sekunden}}$ }\)

​ Trigonometric Identities - 2

\(\text{Formula } 1: \boxed{\sin(A+B) = \dfrac{2\cdot \tan \left(\frac{A+B}{2} \right)} {1+\tan^2\left(\frac{A+B}{2} \right) } }\\ \text{Formula } 2: \boxed{\cos(A)-\cos(B) = -2\sin\left(\frac{A+B}{2} \right)\sin\left(\frac{A-B}{2} \right) } \\ \text{Formula } 3: \boxed{\sin(A)-\sin(B) = 2\cos\left(\frac{A+B}{2}\right)\sin \left(\frac{A-B}{2} \right) } \)

\(\begin{array}{|rcll|} \hline \dfrac{p}{q} &=& \dfrac{\cos(A)-\cos(B) } {\sin(A)-\sin(B) } \\\\ &=& \dfrac{-2\sin\left(\frac{A+B}{2} \right)\sin\left(\frac{A-B}{2} \right) } { 2\cos\left(\frac{A+B}{2}\right)\sin \left(\frac{A-B}{2} \right) } \\\\ &=& - \tan \left(\frac{A+B}{2} \right) \\ \mathbf{\tan \left(\frac{A+B}{2} \right)} &\mathbf{=}& \mathbf{- \dfrac{p}{q}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \sin(A+B) &=& \dfrac{2\cdot \tan \left(\frac{A+B}{2} \right)} {1+\tan^2\left(\frac{A+B}{2} \right) } \\\\ &=& \dfrac{2\cdot \left( \dfrac{-p}{q} \right) } {1+\left( \dfrac{-p}{q} \right)^2 } \\\\ &=& -\dfrac{2\cdot p } {q\left(1+ \dfrac{p^2}{q^2} \right) } \\\\ &=& -\dfrac{2\cdot p } { q+ \dfrac{p^2}{q } } \\\\ \mathbf{\sin(A+B)} &\mathbf{=}& \mathbf{-\dfrac{2pq } { p^2+q^2 } } \\ \hline \end{array}\)

Another one of my Triangle Questions

In \(\Delta ABC\), line segments are drawn parallel to each of the sides dividing the triangle into six regions.
The areas of three regions are shown in the figure. What is the area of \(\Delta ABC\)?

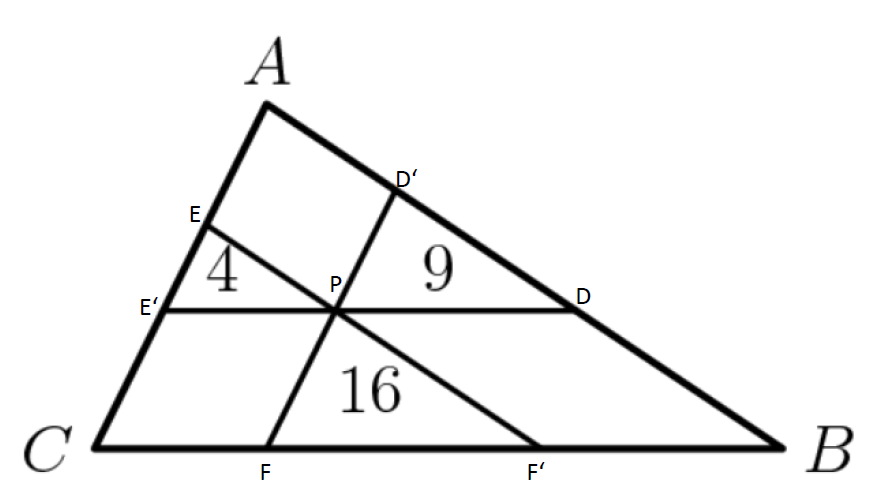
\(\begin{array}{l} \text{Let Area $A =[ABC] $} \\\\ \text{Let Area $A_4=[E'EP] =a^2 = 4, ~a=2 $}\\ \text{Let Area $A_5=[D'DP] =b^2 = 9, ~b=3 $}\\ \text{Let Area $A_6=[F'FP] =c^2 = 16 ~c=4$} \\\\ \text{Let Area $A_1=[E'AD] $}\\ \text{Let Area $A_2=[D'BF] $}\\ \text{Let Area $A_3=[F'CE] $} \end{array}\)

\(\text{The triangles are similar $\\( \triangle ABC \sim \triangle E'EP \sim \triangle D'DP \sim \triangle F'FP \sim \triangle E'AD \sim \triangle D'BF \sim \triangle F'CE )$.} \)

The key theorem we apply here is that the ratio of the areas of 2 similar triangles is
the ratio of a pair of corresponding sides squared.

\(\begin{array}{|rcll|} \hline \dfrac{A_4}{A} &=& \left(\dfrac{E'P}{CB}\right)^2 \\ \dfrac{A_5}{A} &=& \left(\dfrac{PD}{CB}\right)^2 \\ \hline \dfrac{A_4}{A}\cdot \dfrac{A}{A_5} &=& \dfrac{E'P^2}{CB^2} \cdot \dfrac{CB^2}{PD^2} \\ \dfrac{A_4}{A_5} &=& \dfrac{E'P^2}{PD^2} \\ \dfrac{a^2}{b^2} &=& \dfrac{E'P^2}{PD^2} \\ \dfrac{a}{b} &=& \dfrac{E'P}{PD} \\ \boxed{\dfrac{E'P}{PD}=\dfrac{a}{b} } \\ \hline \end{array} \)

\(\begin{array}{|rclcrl|} \hline \dfrac{E'P}{PD} &=& \dfrac{a}{b} && E'P &=& \dfrac{a}{a+b}E'D \\ && && E'D &=& \dfrac{a+b}{a} E'P \\ \dfrac{E'D}{PD} &=& \dfrac{a+b}{a} \cdot \dfrac{E'P}{PD} \\ \dfrac{E'D}{PD} &=& \dfrac{a+b}{a} \cdot \dfrac{a}{b} \\ \boxed{\dfrac{E'D}{PD} = \dfrac{a+b}{b} } \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \dfrac{A_1}{A_5} &=& \left( \dfrac{E'D}{PD} \right)^2 \\ A_1 &=& A_5\left( \dfrac{E'D}{PD} \right)^2 \\ A_1 &=& b^2\left( \dfrac{a+b}{b} \right)^2 \\ \mathbf{A_1} & \mathbf{=} & \mathbf{(a+b)^2} \quad & | \quad A_1 = (2+3)^2=5^2=25 \\ \hline \end{array} \)

analogous

\(\begin{array}{|rclcrl|} \hline \dfrac{D'P}{PF} &=& \dfrac{b}{c} && D'P &=& \dfrac{b}{b+c}D'F \\ && && D'F &=& \dfrac{b+c}{b}D'P \\ \dfrac{D'F}{PF} &=& \dfrac{b+c}{b} \cdot \dfrac{D'P}{PF} \\ \dfrac{D'F}{PF} &=& \dfrac{b+c}{b} \cdot \dfrac{b}{c} \\ \boxed{\dfrac{D'F}{PF} = \dfrac{b+c}{c} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \dfrac{A_2}{A_6} &=& \left( \dfrac{D'F}{PF} \right)^2 \\ A_2 &=& A_6\left( \dfrac{D'F}{PF} \right)^2 \\ A_2 &=& c^2\left( \dfrac{b+c}{c} \right)^2 \\ \mathbf{A_2} & \mathbf{=} & \mathbf{(b+c)^2} \quad & | \quad A_2 = (3+4)^2=7^2=49 \\ \hline \end{array}\)

analogous

\(\begin{array}{|rclcrl|} \hline \dfrac{F'P}{PE} &=& \dfrac{c}{a} && F'P &=& \dfrac{c}{a+c}F'E \\ && && F'E &=& \dfrac{a+c}{c}F'P \\ \dfrac{F'E}{PE} &=& \dfrac{a+c}{c} \cdot \dfrac{F'P}{PE} \\ \dfrac{F'E}{PE} &=& \dfrac{a+c}{c} \cdot \dfrac{c}{a} \\ \boxed{\dfrac{F'E}{PE} = \dfrac{a+c}{a} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \dfrac{A_3}{A_4} &=& \left( \dfrac{F'E}{PE} \right)^2 \\ A_3 &=& A_4\left( \dfrac{F'E}{PE} \right)^2 \\ A_3 &=& a^2\left( \dfrac{a+c}{a} \right)^2 \\ \mathbf{A_3} & \mathbf{=} & \mathbf{(a+c)^2} \quad & | \quad A_3 = (2+4)^2=6^2=36 \\ \hline \end{array} \)

\(\mathbf{A=\ ?}\)

\(\begin{array}{|rcll|} \hline A_1+A_2+A_3 &=& \mathbf{A}+ A_4+A_5 + A_6 \\ 25+49+36 &=& A+ 4+9+16 \\ 110 &=& A + 29 \\ A &=& 110 - 29 \\ \mathbf{A} & \mathbf{=} & \mathbf{81} \\ \hline \end{array}\)

How many degrees are in the smaller angle formed by the minute and hour hands on a clock at 12:30?

\(\boxed{\large{\Delta\varphi=330\cdot t}} \\~ \text{$t$ is the time in hours }\\~ \text{$\Delta\varphi$ is the angle in degrees between minute and hour hands. }\)

\(\text{time at $12:30$ } \)

\(\begin{array}{|rcll|} \hline t &=& 12+\dfrac{30}{60} = 12.5 \ h \\ \Delta\varphi &=& 330 \cdot 12.5 \\ &=& 4125^{\circ} \\ \Delta\varphi &=& 4125^{\circ} - 11\cdot 360^{\circ} \\ && \text{A multiple of $360^{\circ}$ degrees must be deducted from the angle.}\\ \Delta\varphi &=& 4125^{\circ} - 3960^{\circ} \\ \mathbf{\Delta\varphi} &\mathbf{=}& \mathbf{165^{\circ}} \\ \hline \end{array}\)

The smaller angle formed by the minute and hour hands on a clock at 12:30 are \(\mathbf{165^{\circ} }\)

Given that n>1, what is the smallest positive integer n whose positive divisors have a product of n^6?

\(\text{If $n$ is not a perfect square, the divisors of n are divided into couples.} \\ \text{For example, the divisors of $12$ are $1, 2, 3, 4, 6,$ and $12$.} \\ \text{$d(12)$ is $6$, and $1·2·3·4·6·12=1728=123=1262=12^{\frac{d(n)}{2}}$} \\ \text{In our example, $1$ and $12$ are partners, as are $2$ and $6$, as are $3$ and $4$.} \\ \text{Note that the product of any $2$ partnered numbers is $n$.} \\ \text{Then there are \frac{d(n)}{2} couples. } \\ \text{The product of the elements in any couple is $n$, } \\ \text{so the product of all the divisors of $n$ is $ n^{ \frac{d(n)}{2}}$.}\)

\(\text{The divisors have a product of $n^6$, so $n^6=n^{ \frac{d(n)}{2}}$, or $6 = \frac{d(n)}{2}$ } \\ \text{So we see $\mathbf{d(n) = 12}$. Our number $n$ must have $\mathbf{12}$ divisors! }\)

\(\text{The factorisation of $12$ is ${\color{red}3}\cdot {\color{red}2}\cdot {\color{red}2}$} \\ \text{$d(n) = (\underbrace{{\color{blue}2}+1}_{={\color{red}3}}) (\underbrace{{\color{blue}1}+1}_{={\color{red}2}}) (\underbrace{{\color{blue}1}+1}_{={\color{red}2}}) =12, $} \\ \text{so the factorisation of $ n = p_1^{\color{blue}2}p_2^{ \color{blue}1 }p_3^{ \color{blue}1 } $ } \\ \text{The smallest prime numbers are $p_1=2,~p_2=3$ and $p_3=5$ } \\ \text{So the number $n = 2^{\color{blue}2}3^{ \color{blue}1 }5^{ \color{blue}1 } = \mathbf{60} $ }\)

matrix help

\(\text{Formula: $\boxed{MM^{-1}=I}$}\)

\(\begin{bmatrix} 5&-7\\ -2 & 3 \end{bmatrix} \begin{bmatrix} 3&7\\ 2 & 5 \end{bmatrix} = \begin{bmatrix} 1& 0\\ 0 & 1 \end{bmatrix} \)

so A

Für einen Induktionsbeweis soll im letzten schritt folgende Rechnung vereinfacht werden.

\(\begin{array}{rclrcl} && 3^{n+1} - 36\cdot \sum\limits_{k=0}^{n-3} (3^k) - 16 \\ &=& 3^n3^1 - 36\cdot \sum\limits_{k=0}^{n-3} (3^k) - 16 \\ &=& 3\cdot 3^n - 36\cdot \underbrace{\sum\limits_{k=0}^{n-3} (3^k)}_{\text{geometrische Reihe}} - 16 \\ \end{array} \)

\(\qquad \begin{array}{rclrcl} && &s = \sum\limits_{k=0}^{n-3} (3^k) &=& 1+3^1+3^2+\ldots + 3^{n-4}+3^{n-3} \\ && &3s &=& 3^1+3^2+\ldots + 3^{n-4}+3^{n-3}+3^{n-2} \\ \hline &&& s-3s &=& 1-3^{n-2} \\ &&& 3s-s &=& 3^{n-2} - 1 \\ &&& 2s &=& 3^{n-2} - 1 \\ &&& s &=& \dfrac{3^{n-2} - 1}{2} \\ && & \mathbf{\sum\limits_{k=0}^{n-3} (3^k)} & \mathbf{=} & \mathbf{\dfrac{3^{n-2} - 1}{2}} \\ \end{array} \)

\(\begin{array}{rclrcl} &=& 3\cdot 3^n - 36\cdot \dfrac{3^{n-2} - 1}{2} - 16 \\ &=& 3\cdot 3^n - 18\cdot (3^{n-2} - 1) - 16 \\ &=& 3\cdot 3^n - 18\cdot 3^{n-2} +18- 16 \\ &=& 3\cdot 3^n - 18\cdot 3^n3^{-2} + 2 \\ &=& 3\cdot 3^n - \dfrac{18\cdot 3^n}{9} + 2 \\ &=& 3\cdot 3^n - 2\cdot 3^n + 2 \\ &\mathbf{=}& \mathbf{ 3^n + 2 } \\ \end{array}\)

\(\large 3^{n+1} - 36\cdot \sum\limits_{k=0}^{n-3} (3^k) - 16 = \color{red}3^n + 2 \)

Write recursive rule for sequence

1)

7, 20, 33, 46, 59.....

\(\begin{array}{|rcll|} \hline & \text{difference} \\ \hline 7 \\ & \color{red}13 \\ 20 \\ & \color{red}13 \\ 33 \\ & \color{red}13 \\ 46 \\ & \color{red}13 \\ 59 \\ \hline \end{array}\)

This is a Arithmetic Sequence

\(\text{Formula:}~ \boxed{a_n=a_1 + (n-1)d,\text{ with } a_1=7\text{ and }d = 13 }\)

\(\begin{array}{ll} \text{where:}\\ & a_1~ \text{ is the first term, and} \\ & d~ \text{ is the difference between the terms (called the "common difference")} \\ \end{array}\)

Write recursive rule

\(\begin{array}{|rcll|} \hline a_n &=& a_1 + (n-1)d \\ a_{n+1} &=& a_1 + \Big((n+1)-1 \Big)d \\ \hline a_{n+1}-a_n &=& a_1 + \Big((n+1)-1 \Big)d - \Big( a_1 + (n-1)d \Big) \\ a_{n+1}-a_n &=& a_1 + nd - a_1 - (n-1)d \\ a_{n+1}-a_n &=& a_1 + nd - a_1 - nd +d \\ a_{n+1}-a_n &=& d \quad & | \quad +a_n \\ \mathbf{a_{n+1}} & \mathbf{=} & \mathbf{a_n+ d} \qquad d=\color{red}13 \\ \mathbf{a_{n+1}} & \mathbf{=} & \mathbf{a_n+\color{red}13} \\ \hline \end{array} \)

How many of the positive divisors of 3240 are multiples of 3?

\(\text {The prime factors of $\mathbf{3240= 2^{\color{red}3} \cdot 3^{\color{red}4} \cdot 5^{\color{red}1} }$ } \\ \text {The positive divisors of $3240$ are $\mathbf{({\color{red}3}+1)({\color{red}4}+1)({\color{red}1}+1) = 40 }$ } \)

\(\text{How many of the positive divisors of $3240$ are $\textbf{not}$ multiples of $3$ ?}\)

\(\begin{array}{|ccccccl|} \hline 2^3 && 3^4 && 5^1 \\ \begin{Bmatrix} 2^0 \\ 2^1 \\ 2^2 \\ 2^3 \end{Bmatrix} && \begin{Bmatrix} 3^0 \end{Bmatrix} && \begin{Bmatrix} 5^0 \\ 5^1 \end{Bmatrix} \\ 4 & \times& 1 & \times& 2 &=& \mathbf{8} \\ \hline \end{array}\)

\(\text{How many of the positive divisors of $3240$ are multiples of $3$ ?}\)

\(\mathbf{40-8 = 32} \)

\(\text{There are $\mathbf{32}$ positive divisors of $3240$, which are multiples of $3$.}\)

If Log(5) = a, and Log(2) = b, determine Log(125) + Log(8) in terms of a and b

\(\begin{array}{|rcll|} \hline \boxed{125 = 5^3 \\ 8 = 2^3} \\ && \log(125) + \log(8) \\ &=& \log(5^3) + \log(2^3) \quad & \quad \boxed{\log(a^b) = b\times\log(a)} \\ &=& 3\times \log(5) + 3\times \log(2) \quad & \quad \log(5) = a,~ \log(2)=b \\ &=& 3\times a + 3\times b \\ &\mathbf{=}& \mathbf{3\times (a + b)} \\ \hline \end{array}\)