MaxWong

$\quad \log_{1/2} \left(16\cdot 5 \cdot \dfrac1{10}\right)\\ = \log_{1/2} 8\\ = \dfrac{\log_2 8}{\log_2 \dfrac12}\\ =\dfrac3{-1}\\ = -3$

$\displaystyle xy + x = \frac{3x + 2y + z + y + 2z}{3}\\ xy + x = x + \dfrac{2y}3 + \dfrac z3 + \dfrac y3 + \dfrac{2z}3\\ xy + x = x + y + z\\ xy = y + z\\ x = \dfrac{y + z}y$

$\displaystyle \frac{a}{3} + 1 = \frac{a + 3}{a} + 1\\ \dfrac a3 + 1 = 2 + \dfrac 3a\\ \dfrac a3 - \dfrac3a - 1 = 0\\ \left(\dfrac a3\right)^2 - \dfrac a3 - 1 = 0\\ \dfrac a3 = \dfrac{1 \pm \sqrt 5}2\\ a = \dfrac{3(1 \pm \sqrt 5)}2$

So the values of a are 3 times the golden ratio, or 3 times the negative reciprocal of the golden ratio. Nice!

Recall the compound angle formula: 

$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B\\ \cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$

We then have:

$\quad \cos C\\ = \cos(180^\circ - A - B)\\ = -\cos(A + B)\\ =-\cos A \cos B + \sin A \sin B\\ =-\sqrt{\dfrac7{10}} \sqrt{\dfrac{3}{10}} + \sqrt{1 - \left(\sqrt{\dfrac7{10}}\right)^2} \cdot \sqrt{1 - \left(\sqrt{\dfrac3{10}}\right)^2}\\ =-\sqrt{\dfrac7{10}} \sqrt{\dfrac{3}{10}}+\sqrt{\dfrac7{10}} \sqrt{\dfrac{3}{10}}\\ = 0$

This shows that $\triangle ABC$ is a right triangle with $\angle C = 90^\circ$.

Simplifying, we have $(3y - 11)^4$.

So the coefficient of $y^4$ is $3^4 = 81$

Extract the useful information: M is the midpoint of BC. 

Then triangle AMC has half the base of triangle ABC, and the same height. 

The area of triangle AMC would be half that of triangle ABC, so the answer is 90.

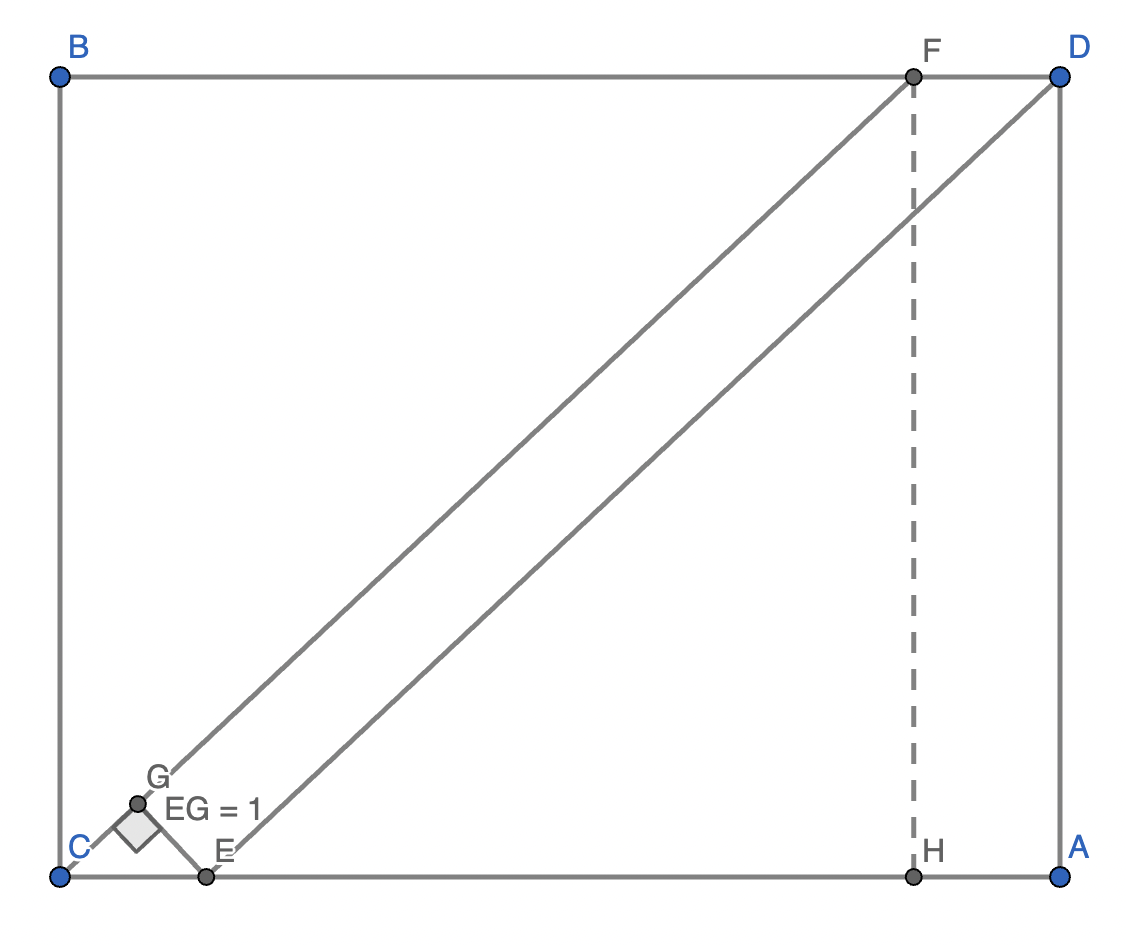
Label the diagram as shown. Let $\angle FCE = \theta$ and $EC = x$.

Let H be a point on AC such that FH is perpendicular to AC. Then $FH = 8$.

Note that $CE = FD = HA = x$. Then $CH = 10 - x$. 

$CF = \sqrt{8^2 + (10 - x)^2} = \sqrt{x^2 - 20x + 164}$ by using Pythagoras theorem in $\triangle CFH$.

In $\triangle ECG$, $\sin \theta = \dfrac{EG}{EC} = \dfrac1x$.

In $\triangle FHC$, $\sin \theta = \dfrac{FH}{CF} = \dfrac8{\sqrt{x^2 -20x+164}}$.

So we have $\dfrac1x = \dfrac8{\sqrt{x^2 - 20x + 164}}$. Squaring gives $\dfrac1{x^2} = \dfrac{64}{x^2 - 20x + 164}$.

Rearranging, 

$64x^2 = x^2 - 20x + 164\\ 63x^2 + 20x - 164 = 0\\ x = \dfrac{-20 \pm \sqrt{20^2 - 4(63)(-164)}}{2(63)}\\ x = \dfrac{8 \sqrt{163} - 10}{63}\text{ (reject negative root)}$

Hence, the area is $\dfrac{8x}2 = \dfrac{32 \sqrt{163} - 40}{63}$.

This is wrong, but I can't edit it, see CPhill's answer below

... and let $X$ be a point such that $MH = MX$, as shown below

Did you forget to attach a diagram?

Suppose O is the centre of the circle. Then $\Delta OP_1 P_2$ is an isosceles triangle with $OP_1 = OP_2 = 1$ and $\angle P_1OP_2 = \dfrac{360^\circ}{10} = 36^\circ$.

Then $P_1P_2 ^2 = 1^2 + 1^2 - 2(1)(1) \cos 36^\circ = 2 - \dfrac{1 + \sqrt 5}2 = \dfrac{3 - \sqrt 5}2\\ $. Note that $\left(\dfrac{\sqrt 5 - 1}2\right)^2 = \dfrac{3 - \sqrt 5}2$. Then $P_1P_2 = \dfrac{\sqrt 5 - 1}2$.

Repeating the same process 10 times gives $P_1 P_2 + P_2 P_3 + P_3 P_4 + \cdots + P_9 P_{10} + P_{10} P_1 = 10\cdot \dfrac{\sqrt 5 -1}2 = 5(\sqrt 5 - 1)$.