Hi Gibson338 :)
Find the absolute maximum and absolute minimum values of f in the given interval.
f(t)=t+cot(t/2) [pi/4, 7pi/4]
pi/4 = 0.7853981633974483
7pi/4 = 5.4977871437821382
end points
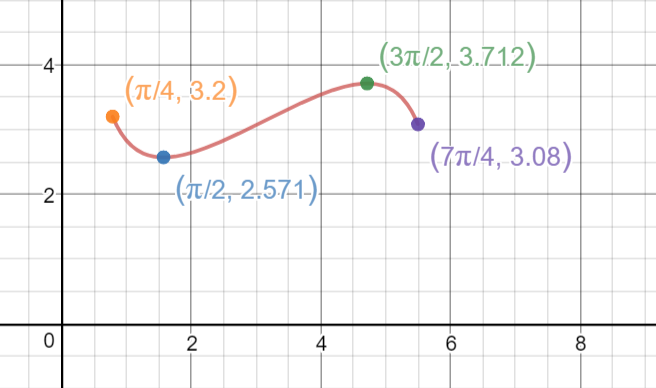
f(pi/4)=pi/4+cot(pi/8) = pi/4+cot(pi/8) = 3.20
f(7pi/4)= 7pi/4+cot(7pi/8) = 7pi/4+cot(7pi/8) = 3.08
end points function values are approx 3.2 and 3.08
\(\text{Firstly cot(t/2) must be defined}\\ so\;\; sin(t/2) \ne0\\ so \;\;t/2\ne n\pi \qquad where\;\;n\in Z\\ so \;\;t\ne 2n\pi \qquad where\;\;n\in Z\)
\(f(t)=t+cot(t/2)\\ let\;\;y=f(t)\\ y=t+\frac{cos(t/2)}{sin(t/2)}\\ let\\ u=cos(t/2) \qquad \\ \frac{du}{dt}=0.5*-sin(t/2)\\ \frac{du}{dt}=-0.5sin(t/2)\\~\\ v=sin(t/2)\\ \frac{dv}{dt}=0.5*cos(t/2)\\~\\ \frac{dy}{dt}=1+\frac{vu'-uv'}{v^2}\\ \frac{dy}{dt}=1+\frac{sin(t/2)[-0.5sin(t/2)]-cos(t/2)0.5(cos(t/2)}{sin(t/2)^2}\\ \frac{dy}{dt}=1+\frac{-0.5sin^2(t/2)-0.5(cos^2(t/2)}{sin(t/2)^2}\\ \frac{dy}{dt}=1+\frac{-0.5}{sin(t/2)^2}\\\)
Find stat points that is when dy/dt = 0
\(0=1+\frac{-0.5}{sin(t/2)^2}\\ 1=\frac{0.5}{sin(t/2)^2}\\ sin(t/2)^2=0.5\\ sin(t/2)=\pm\sqrt{0.5}\\ \frac{t}{2}= n\pi \pm \frac{\pi}{4}\\ t= 2\pi n\pm \frac{\pi}{2}\\ \)
but
\(\frac{\pi}{4} \le t \le \frac{7\pi}{4}\\ t=\frac{\pi}{2}\;\;or \;\;\frac{3\pi}{2}\\ \text{So the stationary points are }\\ (\frac{\pi}{2},2.571),\quad (\frac{3\pi}{2},3.712) \)
\(end\; points\; ( \frac{\pi}{2}, 3.20) \;\;and \;\; ( \frac{7\pi}{4}, 3.08) \)
So the absolute minimum is approx 2.571 when t=pi/2
and the absolute maximum is approx 3.712 when t=3pi/2
Here is the graph: