1. Given f(x)=3ax^2+2bx+x with a≠0, when 0≤x≤1 |f(x)|≤1, please determine the maximum value of a.
f(0)=0
f(1)=3a+2b+1
\(-1\le3a+2b+1\qquad and \qquad 3a+2b+1\le+1\\ -2\le3a+2b\qquad and \qquad 3a+2b\le0\\ -2-2b\le3a\qquad and \qquad 3a\le-2b\\ \frac{-2-2b}{3}\le a\qquad and \qquad \qquad a\le\frac{-2b}{3}\\ \frac{-2b}{3}-\frac{2}{3}\le a\qquad and \qquad \qquad a\le\frac{-2b}{3}\\ \frac{-2b}{3}-\frac{2}{3}\le a\le\frac{-2b}{3}\\ \)
I want the biggest 'a' so it follows that
\(a=\frac{-2b}{3}\\ b=-\frac{3a}{2}\)
It also follows that a is positive and b is negative
so the question becomes
\( f(x)=3ax^2+2bx+x \\ f(x)=3ax^2+2*\frac{-3a}{2}x+x \\ f(x)=3ax^2-3ax+x \\ or\\ f(x)=x(3ax-3a+1) \)
with a≠0, when 0≤x≤1 |f(x)|≤1, please determine the maximum value of a.
and f(1)= 3a+2b+1 = 3a-3a+1 = 1
So f(x) is a concave up parabola passing through (0,0) and (1,1)
\(f'(x)=6ax-3a+1\\ stat\;pt \;is\;when\; f'(x)=0\\ 6ax-3a+1=0\\ 6ax=3a-1\\ x=\frac{3a-1}{6a}\\ or\\ x=\frac{1}{2}-\frac{1}{6a}\\ \)
Now a is positive and as big as possible so I am going to assume that an 'a' exists such that
the stationary point will lie between x=0 and x=0.5
This means that the stationary point (minimim) lies in the designated region of the graph.
So the minimum value must be greater than or equal to -1 (we already know it is less than 1)
The minimum value of f(x) is
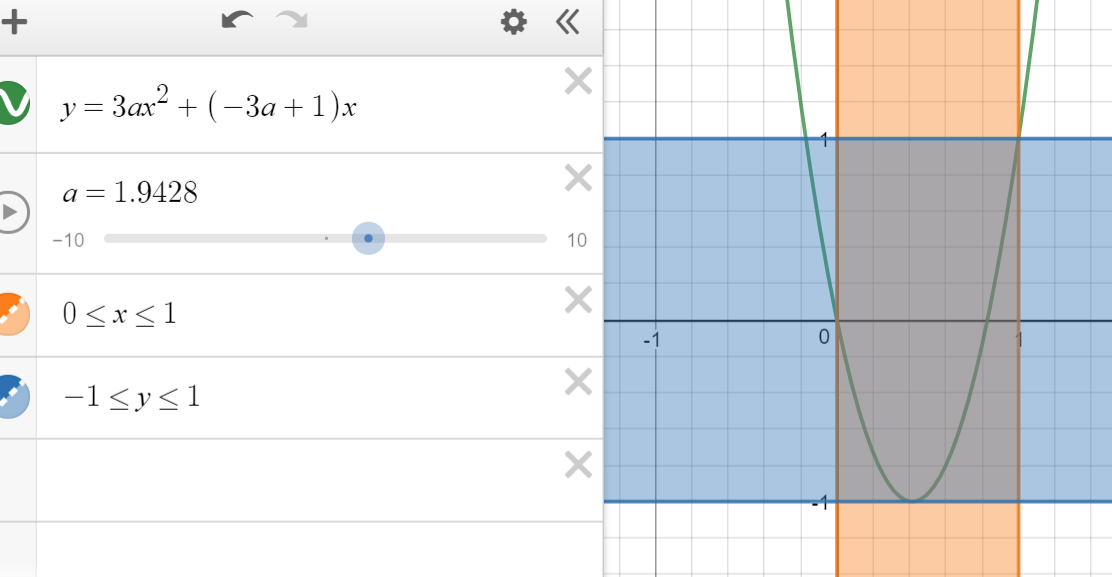
\(f(\frac{3a-1}{6a})=\frac{3a-1}{6a}[(3a*\frac{3a-1}{6a})-3a+1]\ge-1\\ \frac{3a-1}{6a}[(\frac{3a-1-6a+2}{2})]\ge-1\\ remembering \;that\;a>0\\ (3a-1)(3a-1-6a+2)\ge-12a\\ (3a-1)(-3a+1)\ge-12a\\ (3a-1)(3a-1)\le12a\\ 9a^2-6a+1\le12a\\ 9a^2-18a+1\le0\\ \text{If this was set to y it would be a concave up parabola so} \\\text{ the function will be less than zero between the roots. } \\\text{Find the roots.}\\ a=\frac{18\pm\sqrt{324-36}}{18}\\ a=1\pm\frac{2\sqrt{2}}{3}\\ \text{So the biggest value of a is}\\ a=1+\frac{2\sqrt{2}}{3}\\ a\approx 1.9428 \)
Here is the graph