A water trough is 7 m long and has a cross-section in the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of 0.3 m3/min how fast is the water level rising when the water is 40 cm deep?
I am going to refer to depth as height (h). It is much less confusing than d would be.
We are given the dimensions of the trough and we are given \(\frac{dV}{dt}\\ \)
We are asked to find \(\frac{dh}{dt}\) when h = 0.4 metres.
Now
\(\frac{dh}{dt}=\frac{dh}{dV}\times \frac{dV }{dt}\\ \frac{dh}{dt}=\frac{dh}{dV}\times 0.3\\\)
So can I find dh/dV?
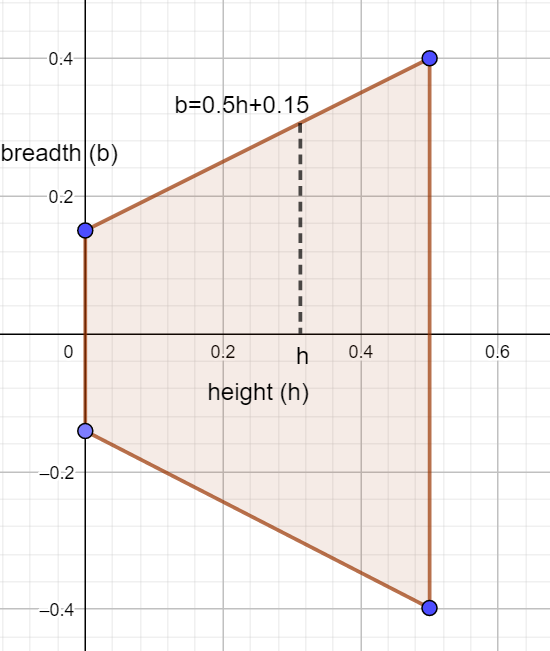
The pic shows the area cross section of the trough. (it is sideways)
Presenting it like this it was easy to find that the eqation of the side is b=0.5h+0.15
For any specific height h the surface area is a rectangle. the length is 7m, the breadth is 2(0.5h+0.15)
So the surface area is
\(S=7*2(0.5h+0.15)\\ S=7h+2.1\\~\\\)
\(Volume\\ V=\frac{1}{2}*2*(0.15+\frac{h}{2}+0.15)*h*7\\ V=(0.3+\frac{h}{2})*7h\\ V=2.1h+\frac{7h^2}{2}\\ \\~\\ \frac{dV}{dh}=7h+2.1\\ \frac{dh}{dV}=\frac{1}{7h+2.1}\\~\\ when\;\;h=0.4m\\ \frac{dh}{dV}=\frac{1}{7*0.4+2.1}=\frac{1}{4.9}=\frac{10}{49}\\\)
\(\frac{dh}{dt}=\frac{dh}{dV}\times \frac{dV }{dt}\\ \frac{dh}{dt}=\frac{10}{49}\times 0.3\\ \frac{dh}{dt}=\frac{3}{49} \; m/s\\\)
At the instant when the water is 0.4 metres deep the water is rising at \(\frac{3}{49}\;\;m/sec\)
This could easily be riddles with errors, you had best check it very carefully.