Melody

Hi Guest,

No one thinks that you are cheating.

We need more honest people like you on this forum.

Why don't you join up and get yourself known to people.

Its free and there are some benefits, like being able to send private messages and also being able to track your questions more easily.

Here is a reasonably accurate pic, (unless I have done something super stupid)

If you know a bit of trig it should be easy for you to work out the needed radius now.

Thanks EP.

It was a bit confusing. I just like drawing these pics and if I can get the pic right then I have some chance of answering the question.

Although I will admit that Chris is better at geometry than I am.

It took me AGES to draw it!    

Hi Magic Kitten,

Mostly mods get rid of garbage, like really bad posts, and they tick off answers. 

Just because they are ticked off soen't have to mean that the answer is right. We don't have time to check everything.

That is about it.

If you ever want to ask questions about a post always do so. 

Even if it is ticked off you can still ask question. :)

After a period of time, questions get blocked so you can't answer any more but you only have to send a private message to a mod and they can unlock it for you.

I have probably just done your homework for you.

I hope you can at least learn something from my answer.

Randy presses RAND on his calculator twice to obtain two random numbers between 0 and 1. Let p be the probability that these two numbers and 1 form the sides of an obtuse triangle. Find 4p.

If I draw a square that is 1 by 1 unit. Then every possible outcome  is represented inside that square.

I mean (x,y) in tha square will represent every possible combination of the 2 random numbers.

x is one of the numbers and y is the other one.

Now I need to determine what restrictions will make this true.

Since both these numbers are between 0 and 1 it follows that 1 must be the longest side of the triangle.

Condition 1   For it to be a triangle at all, the 2 random numbers must add to more than 1

then x+y>1

y>-x+1

I have to graph that region.

Condition 2   For it to be an obtuse angled triangle x^2 +y^2 must be less than 

See the pic below to try and understand why this is true.

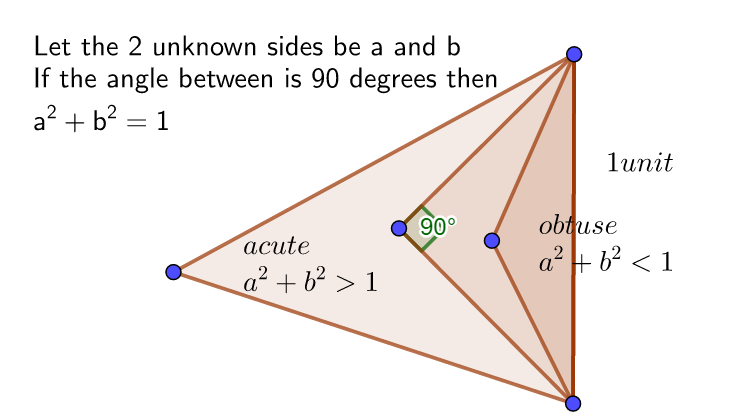
So \(x^2+y^2<1\)

I'll graph that too.

So here is my probability contour graph.

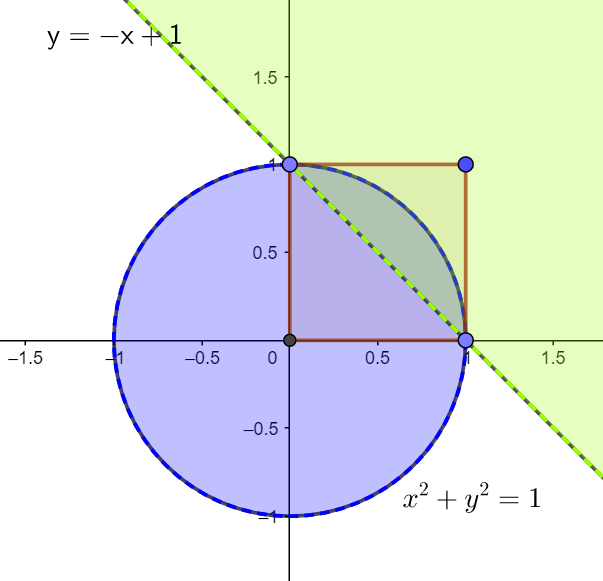
The entire sample space, (that is all possible outcomes) are in the 1 by 1 square.

The green area represents all the points that could make any triangle. with the other long side being 1

The purple area represents all the points that would NOT make an acute angled triange.

So I need to work out the are of the intersection.

\(Area = \frac{\pi r^2}{4}-0.5*1*1\\ Area = \frac{\pi}{4}-0.5\\ Area = \frac{\pi-2}{4}\;units \;squared\\\)

Since the are of the sample space is 1*1=1

The probabilty that I will be able to form the triangle described is    

\(P (\text{That an obtuse angle with 3rd side equal 1 can be formed})=\displaystyle \frac{\pi-2}{4}\)

OH this is not quite what the question asked .. You can finish it.   

Because I had started an answer but not finished it so i hid it until I had time to finish it later.

The ability to do this is one of the perks of being a moderator.

Ususally when there is less answers than is indicated it is becasue one or more of the answers has been hidden either automatically or by a moderator because it is inappropriate or because it needs to be checked for suitablility.

For instance:

Many posts with links are automatically blocked until a mod deems it suitable.

Hi Sketchy,

I have used the same logic as the other person but i have added a few extra words.

So if you can understand.

Feel free to ask questions or comment.

The least positive integer that is divisible by 2,3,4 and 5 and is also a perfect square, perfect cube, 4th power, and 5th power, can be written in the form a^b for positive integers a and b.

What is the least possible value of a+b?

The answer is 90

The number is a^b where  a   is the smallest number that will work.

For instance  4^3 is not ok because 4 = 2^2 so    4^3 can be written as 2^6

This is not worded well but more exact wording would probably just add to confusion anyway.

a^b is a square number so b is a multiple of 2

a^b is a cubic number so b is a multiple of 3

a^b is a power of 5 so b is a multiple of 5

a^b is a power of 4 so b is a multiple of 4 but it is already a multiple of 2 so we just need one more 2

That is

b=2*3*5*2 = 60      It could be bigger but that is the smallest it can be.

Now what number to the power of 60 is a multiple of 2,3,4 and 5

2^60 is not a multiple of 3 or  5 but it is a multiple of 2 and 4

(2*3)^60 is not a muliple of 5 but it is a muliple of 2,3 and 4

(2*3*5)^60 is a muliple of 2 and 3 and 4 and 5. 

so the smallest values of a and b are  30 and 60 respectively

a+b = 30+60 =90

Chris you have answered over me for no good reason AND you left out the bit that would cause the most problem.

"Why is the length of the square 4 units and what has a triangle got to do with a square."

If this kid sees your  answer and wants to learn from it at all, which is quite unlikely, those are the questions they would be asking themselves.

I do admit my answer was very basic but it at least gave a hint on how to find the length of the triangle legs.

If the child wanted more help he/she should have, and probably would have asked.

This is a good question, it has made me think.  

let the legs be x units long

Use pythagoras's theorum to solve for x.

Then you can find the area.