Equation: y = -2 cos 4 x + 3
Desmos Graph: https://www.desmos.com/calculator/e5jilhrvfk
---------------------------------------------------------------------------------------------------------------------------------
- Questions -
1) Midline: y = 3 yes
2) Topline: 5 y=5 It is a line!
3) Bottom Line: 1 y=1
4) Wavelength: π/2 2pi/4 = pi/2 GOOD
5) Quarter Of The Wavelength: π/4 X one quarter of pi/2 IS NOT pi/4 \(\frac{1}{4}*\frac{\pi}{2}=\frac{\pi}{8}\)
6) What would be sensible points for the x-axis? π/4, 3π/4, 5π/4, 7π/4, 9π/4 (?)
pi/8, 2pi/8=pi/4, 3pi/8, 4pi/8=pi/2 etc
7) Will it start on the midline, above or under, why? It will start below the midline because it is a cos graph.
NO Sin graphs start in the middle because sin0=0
+cos0=1 -cos0=-1 This equation has the minus sign so it will start (cross the y axis) at the bottom.
8) Will is start going down or going up, why? It has begun at its lowest point as a cos graph and will begin upwards.
Up because it is is already at the bottom.
9) y-intercept: 1 YES (this is the bottom!)
10) Plot 4 (or 5) points in advance just by knowing what the properties of the graph will be.
I mean maxima, minima, and points on the midline: (π/8, 3), (3π/8, 3), (5π/8, 3), (7π/8, 3), (9π/8, 3) [Or] (π/4, 5), (3π/4, 5) [Etc] (0,1)
11) Graph it from x = 0 to x = Wavelength: ✔
12) What is the first maxima? (π/4, 5)
13) What is the first minima? (π/2, 1)
14) What are points on the midline? (π/8, 3), (3π/8, 3), (5π/8, 3), (7π/8, 3), (9π/8, 3) (?)
Good but I also wanted the ones at the top and bottom (0,-1), pi/4,5), (pi/2,-1)
Look at the graph.
Hopefully these are all correct! You are getting there :)
You need to do a freehand sketch as you answer the questions. They will complement each other and make it easier.
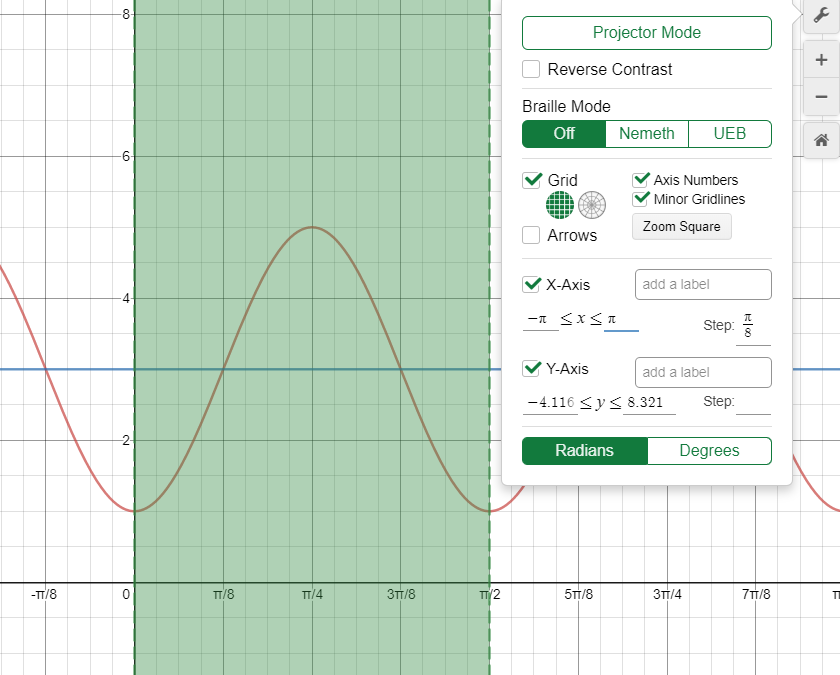
Here is a graph with a better step on the x axis. I have made the x step equal to one quarter of a wave.
https://www.desmos.com/calculator/lh4pzfxeja
I have only added the shaded green so that you can easily see one wavelength.
See how it starts at the bottom.
when x=0 y=-2cos(4*0)+3 = -2*1+3 = 1 (which is at the bottom of the wave)
| y = 7 sin 3 x -6 | |
| Midline | y = -6 correct |
| Topline | 1 (?) correct |
| Bottom line | -13 (?) correct |
| Wavelength | 2π/3 correct |
| Quarter of the Wavelength | π/3 (?) wrong \(\frac{2\pi}{3}\div4 = \frac{\pi}{6} \) |
| What would be sensible points for the x-axis? | As in where it intersects? every quarter like, ... 0, pi/6, 2pi/6 3pi/6, 4pi/6, 5pi/6 .. these fractions should be simplified though |
| Will it start on the midline, above or under, why? | It will start on the midline because it is a sine graph. correct |
| Will is start going down or going up, why? | It will start upwards because of the positive number in front. correct |
| y-intercept | -6 correct |
| Plot 4 (or 5) Points in Advance (I mean maxima, minima, and points on the midline.) | (4π/3, 6) & (3π/2, 1) & (5π/2, -15) & (8π/3, -6) (0,-6) (2pi/3,-6)(pi/3,-6)(pi/6,1)(3pi/6,-13) But it is easier if you do it straight onto the rough graph. |
| Graph it from x=0 to x= wavelength | I'm not sure what this means. I mean graph it by hand for one whole wavelength, starting at the y axis. |
| What is the first maxima? | (π/6, 1) yes |
| What is the first minima? | (π/2, -13) yes |
| What points are on the midline? | (4π/3, 6) & (8π/3, -6) NO you can fix this |
Sorry that I couldn't answer all of these fully or properly I assume, still getting the hang of it.
https://www.desmos.com/calculator/hocp6dfrvm
I just improved the scale of the graph
https://www.desmos.com/calculator/q10ry2yrjp
Also if you hit the region circle on the side you will see one full wavelength.
You can see also how it is divided nicely into 4 quarters.
| y = 3 sin 4 x - 2 | |
| Midline | y = -2 |
| A Maximum Point | (pi/8, 1) |
| A Minimum Point | (3pi/8, -5) |
| Will the y-intercept be top or bottom?
Wavelength | It intercepts at the midline?
pi/2 |
I would love to upload my terrible little sketch graphs, but it's always a pain in the butt to upload them to my computer.
Hopefully these are correct, I tried double-checking them with desmos.
I think I'm starting to make sense of it a little bit better?
Melody: I have put my response in the middle of your answers.
First Question
(please include the question so I don't have to go look for it)
Response to first answer.
y = 4-3 sin (x/4)
The first lowest point should be (2pi, 1) and the first highest point should be (6pi, 7) At least, I think this is correct.
YES, that is perfect, I hope you worked it out with a rough sketch BEFORE you used Desmos.
https://www.desmos.com/calculator/hizjhkehuc I like your graph ![]()
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Second Question
| y = 4 cos (2x) -3 you did this one perfectly | y = f cos (gx) - t | y = f cos (gx) - t melody's correction | ||
| Midline | y = - 3 | y = - t | yes | |
| Amplitude | 4 | f | yes | |
| y-intercept | 1 (-3+4=1) | g x | -t+f | it is easier to get this as you hand sketch the graph |
| Is the y-intercept at the top, middle, or bottom? | Top | Top | yes | |
| Wavelength | π (2pi/2=pi) | 2π (?) x | 2pπ/g | |
| A Maximum Point | (π, 1) | (2π, 0) (?) | (0,-t+f), (2π/g, -t+f) | don't worry about these last 2, they were too hard anyway. |
| A Minimum Point | (π/2, -7) | (π, -2) (?) | (π/g,-t-f) |
I'm not sure how to fill in wavelength, the maximum point, and the minimum point. If you input this into the desmos graph, it gives a rough example, but considering it can be moved due to all these just being variables, I'm just answering with what the baseline graph would look like.
Good, Once you get the wavelength consistently correct that will work well.
anyway those last two questions, max and min with letters was a bit hard, don't get hung up on those.
Please correct me, I think I'm starting to make sense of it more consistently somewhat though.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Note: I do relatively well usually once I make sense of the concept, suddenly something will just click and I understand it. I avoid over-practicing until I feel I have a general sense of what is wrong and right with the material, so that I don't form bad habits or get myself confused. This has been a really great experience having someone work with me one-on-one. I appreciate your patience and willingness a great deal, even if I might be a bit slow.
First Question:
The first highest point should be seven. The first lowest point should be one, correct?
------------------------------------------------------------------------------------------------------------------------------------------------------------------
Second Question:
| y = f cos (gx) -t | |
| Amplitude | f |
| y-intercept | t |
| Midline | y = t |
| Wavelength | (gx)*pi |
With what I'm understanding, we're using these as just placeholders, right? Thus, I can't give any specifics, or am I all wrong?
You have the right idea, but you have made a couple of mistakes.
put some numbers in yourself and see if you can spot your errors. :)
Amplitude is the only one that is completely correct.
| y = sin x | y = sin (2x) | |
| Wavelength | 2π | π |
| Midline | y = 0 | y = 0 |
| Amplitude | 1 | 1 |
| y-intercept | 0 | 0 |
Desmos graph for both equations.
https://www.desmos.com/calculator/c9bimc9kpw
All qualities of both graphs appear to be the same with the exception of wavelength, and so I assume the (2x) affects how the wavelength appears?
| y = 2 sin x + 3 | y = 2 cos x + 3 | |
| Wavelength | 2π | 2π |
| Midline | y = 3 | y = 3 |
| Amplitude | 2 | 2 |
| y-intercept | 3 | 5 |
First Graph: https://www.desmos.com/calculator/dloymhzsxx
Second Graph: https://www.desmos.com/calculator/komjqsqgfi
------------------------------------------------------------------------------------------------------------------
Question 1-
Desmos Graph: https://www.desmos.com/calculator/0ozgnesvrp (From checking afterward.)
a) Midline: y = -1
b) y-intercept: -1
c) Wavelength: π
d) Amplitude: 1
e) Does it start going up or down?: It begins moving upwards.
f) What is the equation?: y = 1 sin x -1
------------------------------------------------------------------------------------------------------------------
Question 2-
Desmos Graph: https://www.desmos.com/calculator/ig7vrwjg8m (From checking afterward.)
a) Midline: y = 4
b) y-intercept: 4
c) Wavelength: π
d) Amplitude: 1
e) Does it start going up or down?: It begins moving downwards.
f) What is the equation?: y = -1 sin x + 4
------------------------------------------------------------------------------------------------------------------
Equation: y = 3 -4 sin x
1. "What is the least confusing way to write this?"
I'm not exactly sure what you mean by that, I apologize.
Are you asking about how can this equation can be rearranged? If so, I'm not entirely sure.
2. "What number does the minus sign belong to?"
The minus sign belongs to the four I presume.
3. "What will be the main features of this graph?"
Once again, not entirely sure what you mean here, I assume you mean the midline, y-intercept, etc?
a) Midline: y = 3
b) y-intercept: 3
c) Wavelength: 2π (From after checking the Desmos graph.)
d) Amplitude: 4
4. "What is the y-intercept?"
The y-intercept is 3.
5. "Is the y-intercept on the centerline?"
It seems to be. (From after checking the Desmos graph.)
6. "From the y-axis, will the graph start going up or down? How can you tell this from the equation?"
I assume it will begin downwards because of the -4 in the equation. Previously, the addition of the minus sign inflects the graph to move downwards initially instead of upwards into the positives. (Accurate after having checked the Desmos graph.)
After checking afterward, here is the graph. https://www.desmos.com/calculator/tmwabdozb0
------------------------------------------------------------------------------------------------------------------
Equation: y = sin x
https://www.desmos.com/calculator/sqqxxosznt
a) Midline: y = 0
b) y-intercept: 0
c) Wavelength: 2π
d) Amplitude: 1
------------------------------------------------------------------------------------------------------------------
Equation: y = -sin x
https://www.desmos.com/calculator/pqi9uqbmyf
a) Midline: y = 0
b) y-intercept: 0
c) Wavelength: 2π
d) Amplitude: -1 (?) No, the amplitude is always positive. It stays +1
What I see from both of these graphs is they share similar properties almost entirely, except for the second graph being flipped. With that said, does that mean the amplitude will be considered -1? Or will it remain a positive always? Either way, they're incredibly similar graphs, but one appears to be flipped because of the negative.
EXCELLENT. If you times by minus -1 the graph flips over, (It reflects across the y axis)
------------------------------------------------------------------------------------------------------------------------------------------------------------------
Equation: y = 3 sin x
https://www.desmos.com/calculator/uluaswag14
a) Midline: y = 0
b) y-intercept: 0
c) Wavelength: 2π
d) Amplitude: 3
------------------------------------------------------------------------------------------------------------------
Equation: y = -3 sin x
https://www.desmos.com/calculator/qw3tpmqfhq
a) Midline: y = 0
b) y-intercept: 0
c) Wavelength: 2π
d) Amplitude: -3 (?) +3
Similarly, comparing these two graphs, the only noticeable difference is that the figure appears to be flipped because of the negative. Once again, I'm not sure if amplitude should ever be written in negatives, and if not, then the answer should be just the definite form of what is already written, I assume. I hope these are correct.
That is all great, you are learning really well.
y= 4(sinx)-3 (I added the equation so it is with the answers - Melody)
a) Midline: y = -3
b) y-intercept: -3
c) Wavelength: 2π
d) Amplitude: 4?
This is the graph from afterward.
https://www.desmos.com/calculator/0znoabjdqu
----------------------------------------------------------------------------------------------------------------------------------------------
Melody:
I am here now so I willl add my response here.
Your answer is spot on.
You seem hesitant about amplitude:
Yes it is 4 and you can see that on the formula.
To get it from the graph find the highest y value and subtract the lowest y value and then halve it. (+1--7)/2 = 8/2 = 4
Or
get the highest y value and subtract the midline y value. In this case +1 - - 3 = 1+3=4
Make sure you underst this from the graph.
-------------------
New question: Get this one right and I will move onto a slightly new idea.
y=6+8sinx
what will be
a) midline
b) y intercept
c) wavelength
d) amplitude
----------------------------------------------------------------------------------------------------------------------------------------------
Peerless Cucumber: *Wave*
y=6+8sinx
a) Midline: y = 6
b) y-intercept: 6
c) Wavelength: 2π
d) Amplitude: 8
https://www.desmos.com/calculator/2miu9weqtv
Here is the graph!
https://www.desmos.com/calculator/gg71ka6oqn
a) Midline: y = 5
b) y-intercept: 5
c) Wavelength: 2π
d) Amplitude: 1
These all are somewhat similar to y = sin x, however, when it becomes +5, it merely moves up 5 on the graph, and the logic seems consistent when replaced by a 2, 3, or any other number, for example. Whereas by changing the number it is multiplied by effects the amplitude?