heureka

Find the derivative of the trig function.

f(t)=t²sint

\(\begin{array}{|rcll|} \hline \mathbf{f(t)} & \mathbf{=} & \mathbf{t^2\sin(t)} \\\\ f'(t) &=& t^2 * \dfrac{d\ \sin(t)}{dt}+ \dfrac{d\ t^2}{dt}*\sin(t) \\\\ && \dfrac{d\ \sin(t)}{dt} = \cos(t) \qquad \dfrac{d\ t^2}{dt}=2t \\\\ f'(t) &=& t^2 *\cos(t) +2t*\sin(t) \\ \mathbf{f'(t)} & \mathbf{=} & \mathbf{ t\Big(2\sin(t) +t\cos(t) \Big) } \\ \hline \end{array}\)

What is the remainder when \((x+1)^{2010}\) is divided by \(x^2+x+1\)?

I assume

Look at the low powers of x.

Eventually they will cycle.

\(\begin{array}{|r|c|c|} \hline n & & \text{remainder} \\ \hline 0 & \dfrac{(x+1)^0}{x^2+x+1} & \color{red}1 \\ \hline 1 & \dfrac{(x+1)^1}{x^2+x+1} & x+1 \\ \hline 2 & \dfrac{(x+1)^2}{x^2+x+1} & x \\ \hline 3 & \dfrac{(x+1)^3}{x^2+x+1} & -1 \\ \hline 4 & \dfrac{(x+1)^4}{x^2+x+1} & -x-1 \\ \hline 5 & \dfrac{(x+1)^5}{x^2+x+1} & -x \\ \hline 6 & \dfrac{(x+1)^6}{x^2+x+1} & \color{red}1 \\ \hline 7 & \dfrac{(x+1)^7}{x^2+x+1} & x+1 \\ \hline 8 & \dfrac{(x+1)^8}{x^2+x+1} & x \\ \hline \ldots &\ldots & \ldots \\ \hline 2010 & \dfrac{(x+1)^{2010}}{x^2+x+1} & \color{red}1 \\ \hline \end{array}\)

\((x+1)^n / (x^2+x+1) \) is cyclic of order 6
So we get \((x+1)^n \equiv (x+1)^{n\pmod{6}}\pmod{x^2+x+1}\)

\((x+1)^{2010} \equiv (x+1)^{6·335+0} \equiv(x+1)^{0} \equiv 1 \pmod{x^2+x+1}\)

The remainder when \((x+1)^{2010}\) is divided by \(x^2+x+1\) is 1

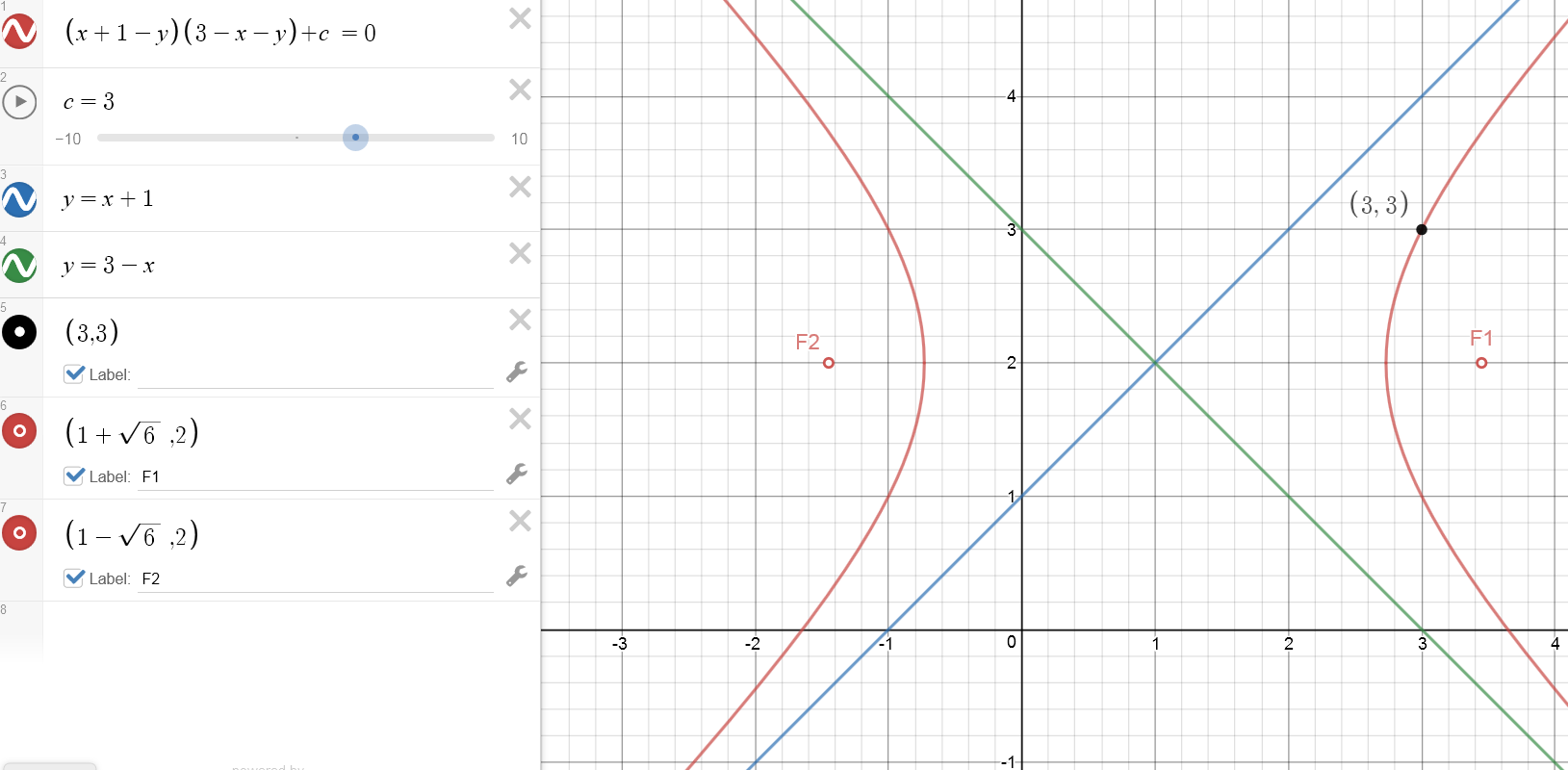
The asymptotes of a hyperbola are y=x+1 and y=3-x. Also, the hyperbola passes through (3,3).
Find the distance between the foci of the hyperbola.

Formula hyperbola:

\(\begin{array}{|l|rcll|} \hline 1. \text{ asymptote} & x+1 &=& y \\ & x+1-y &=& 0 \\\\ \hline 2. \text{ asymptote} & 3-x &=& y \\ & 3-x-y &=& 0 \\\\ \hline \text{hyperbola: } & (x+1-y)(3-x-y) + c &=& 0 \\\\ P(x=3,y=3) & (3+1-3)(3-3-3)+c &=& 0 \\ & (1)(-3)+c &=& 0 \\ & c &=& 3 \\ \text{hyperbola: } &\mathbf{ (x+1-y)(3-x-y) + 3} &\mathbf{=}& \mathbf{0} \\\\ & (x+1-y)(3-x-y) + 3 & = & 0 \\ & \Big((x-y)+1\Big)\Big(3-(x+y)\Big) + 3 & = & 0 \\ & 3(x-y)-(x-y)(x+y)+3-(x+y) + 3 & = & 0 \\ & 3(x-y)-(x-y)(x+y)+3-(x+y) + 3 & = & 0 \\ & 3x-3y-(x^2-y^2)+3-x-y + 3 & = & 0 \\ & 2x-4y-x^2+y^2+6 &=& 0 \quad | \quad \cdot (-1) \\ & x^2-2x -y^2+4y -6 &=& 0 \\ & x^2-2x -y^2+4y &=& 6 \\ & (x-1)^2-1 -(y-2)^2+4 &=& 6 \\ & (x-1)^2 -(y-2)^2 &=& 3 \quad | \quad :3 \\ & \dfrac{(x-1)^2}{3} - \dfrac{(y-2)^2}{3} &=& 1 \\ & \boxed{\text{Formula hyperbola:} \dfrac{ (x-h)^2 }{a^2}- \dfrac{ (x-k)^2 }{b^2} = 1 } \\ & a^2 = 3 \\ & a= \sqrt{3} \\\\ & b^2 = 3 \\ & b= \sqrt{3} \\ \hline \end{array}\)

\(\begin{array}{|l|rcll|} \hline \text{Focus}_1: & F_1(h+ae,k) \\ \text{Focus}_2: & F_2(h-ae,k) \\ \hline \text{Foci distance}: & && h+ae-(h-ae) \\ & &=&h+ae-h+ae \\ & &=& 2ae \quad | \quad e=\dfrac{\sqrt{a^2+b^2}}{a} \\ & &=& 2a\dfrac{\sqrt{a^2+b^2}}{a} \\ & &=& 2 \sqrt{a^2+b^2} \quad | \quad a^2=b^2= 3 \\ & &=& 2 \sqrt{3+3} \\ & &\mathbf{=}& 2 \mathbf{ \sqrt{6} } \\ \hline \end{array}\)

The distance between the foci of the hyperbola is \(\mathbf{2\sqrt{6} }\)

What is the sum of the following sequence: 1000^3 - 999^3 - 998^3 - 997^3 -.............-3^3 - 2^3 - 1^3.

\(\begin{array}{|rcll|} \hline && \mathbf{ 1000^3 - 999^3 - 998^3 - 997^3 -\ldots -3^3 - 2^3 - 1^3} \\ \\ &=& 1000^3 - \left(1^3+2^3+3^3+\ldots +997^3+998^3+999^3 \right) \\ &=& 1000^3 - \left(1 +2 +3 +\ldots +997 +998 +999 \right)^2 \\ &=& 1000^3 - \left(\left(\dfrac{1+999}{2}\right) \cdot 999\right)^2 \\ &=& 1000^3 - 500^2 \cdot 999^2 \\ &=& 1\ 000\ 000\ 000 - 249\ 500\ 250\ 000 \\ &\mathbf{=}& \mathbf{-248\ 500\ 250\ 000} \\ \hline \end{array}\)

Let

\(n\)

and

\(k\)

be positive integers such that \(\dbinom{n}{k}:\dbinom{n}{k + 1} = 4:11\). Find the smallest possible value of .

\(\begin{array}{|rcll|} \hline \dfrac{\dbinom{n}{k}} {\dbinom{n}{k + 1}} &=& \dfrac{4}{11} \quad | \quad \dbinom{n}{k + 1} = \dbinom{n}{k}\cdot \dfrac{n-k}{k+1} \\\\ \dfrac{\dbinom{n}{k}} {\dbinom{n}{k}\cdot \dfrac{n-k}{k+1}} &=& \dfrac{4}{11} \\\\ \dfrac{k+1}{n-k} &=& \dfrac{4}{11} \\\\ 11(k+1) &=& 4(n-k) \\ 11k+11 &=& 4n-4k \\ \mathbf{4n-15k} & \mathbf{=} & \mathbf{11} \\\\ 4n &=& 11+15k \\ n &=& \dfrac{11+15k} {4} \\ &=& \dfrac{11+1-1+15k+k-k} {4} \\ &=& \dfrac{12+16k-(1+k)} {4} \\ &=& \dfrac{12+16k} {4}- \dfrac{(1+k)} {4} \\ &=& 3+4k - \underbrace{\dfrac{(1+k)} {4}}_{=a} \\ \mathbf{n} &\mathbf{=}& \mathbf{3+4k - a} \\\\ a &=& \dfrac{1+k} {4} \\ 4a &=& 1+k \\ \mathbf{k} &\mathbf{=} & \mathbf{4a-1,\quad a\in \mathbb{Z}}\\\\ n &=& 3+4k - a \quad | \quad k=4a-1 \\ &=& 3+4(4a-1) - a \\ &=& 3+16a-4 - a \\ \mathbf{n} &\mathbf{=}& \mathbf{-1+15a} \\\\ n_{min} &=& -1+15\cdot 1\quad | \quad a=1 \\ \mathbf{n_{min}} &\mathbf{=}& \mathbf{14} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline k&=& 4a-1 \quad | \quad a=1 \\ k&=& 4\cdot1 -1 \\ k&=& 3 \\ \dfrac{\dbinom{14}{3}} {\dbinom{14}{4}} &=& \dfrac{4}{11} \\ \hline \end{array}\)

2. 

∫5 3 (1/(x^2-6x+13))dx

\(\large{\int \limits_{3}^{5} \dfrac{1}{ \sqrt{x^2-6x+13} }\ dx}\)

\(\begin{array}{|rcll|} \hline && \mathbf{ \displaystyle \int \limits_{3}^{5} \dfrac{1}{ \sqrt{x^2-6x+13} }\ dx} \\\\ &=& \displaystyle \int \limits_{3}^{5} \dfrac{1}{ \sqrt{(x-3)^2-9+13} }\ dx \\\\ &=& \displaystyle \int \limits_{3}^{5} \dfrac{1}{ \sqrt{(x-3)^2+4} }\ dx \\\\ &=& \displaystyle \int \limits_{3}^{5} \dfrac{1} { \sqrt{ 4 \left( 1+ \dfrac{ (x-3)^2 } {4} \right) } }\ dx \\\\ &=& \displaystyle \int \limits_{3}^{5} \dfrac{1} { 2 \sqrt{ 1+ \left(\dfrac{x-3}{2}\right)^2 } }\ dx \\\\ &=& \dfrac{1}{2} \displaystyle \int \limits_{3}^{5} \dfrac{1} {\sqrt{ 1+ \left(\dfrac{x-3}{2}\right)^2 } }\ dx \\\\ && \quad \boxed{ \text{substitute: } \\ \dfrac{x-3}{2} = \sinh(\theta),\ \dfrac{1}{2}dx=\cosh(\theta)d\theta,\ dx=2\cosh(\theta)d\theta \\ x=3 \Rightarrow \theta=\sinh^{-1}\left(\dfrac{3-3}{2}\right)=0,\\ x=5\Rightarrow \theta=\sinh^{-1}\left(\dfrac{5-3}{2}\right)\\ =\sinh^{-1}(1)=\ln(1+\sqrt{1^2+1})=0.88137358702} \\\\ &=& \dfrac{1}{2} \displaystyle \int \limits_{0}^{0.88137358702} \dfrac{1} {\sqrt{ 1+ \Big(\sinh(\theta)\Big)^2 } }2\cosh(\theta)\ d\theta \\\\ &=& \displaystyle \int \limits_{0}^{0.88137358702} \dfrac{\cosh(\theta)} { \cosh(\theta) }\ d\theta \\\\ &=& \displaystyle \int \limits_{0}^{0.88137358702} d\theta \\\\ &=& \Big[ \theta \Big]_{0}^{0.88137358702} \\\\ &=& 0.88137358702 \\\\ && \mathbf{ \displaystyle \int \limits_{3}^{5} \dfrac{1}{ \sqrt{x^2-6x+13} }\ dx = \sinh^{-1}(1) = 0.88137358702} \\ \hline \end{array}\)

1. 

∫1/6 0 (1/(sqrt(1-9x^2))dx

\(\large{\int \limits_{0}^{\frac{1}{6}} \dfrac{1}{ \sqrt{1-9x^2} }dx}\)

\(\begin{array}{|rcll|} \hline && \mathbf{ \large{\int \limits_{0}^{\frac{1}{6}} \dfrac{1}{ \sqrt{1-9x^2} }\ dx} } \\\\ &=& \displaystyle \int \limits_{0}^{\dfrac{1}{6}} \dfrac{1}{ \sqrt{1-(3x)^2} }\ dx \\\\ && \quad \boxed{ \text{substitute: } \\ u = 3x,\ du=3\ dx,\\ x=0 \Rightarrow u=3\cdot 0=0,\\ x=\dfrac{1}{6}\Rightarrow u=3\cdot \dfrac{1}{6}=\dfrac{1}{2} } \\\\ &=& \displaystyle \int \limits_{0}^{\dfrac{1}{2}} \dfrac{1}{ \sqrt{1-u^2} } \dfrac{du}{3} \\\\ &=& \dfrac{1}{3}\displaystyle \int \limits_{0}^{\dfrac{1}{2}} \dfrac{1}{ \sqrt{1-u^2} }\ du \\\\ && \quad \boxed{ \text{substitute: } \\ u = \sin(\theta),\ du=\cos(\theta)d\theta,\\ u=0 \Rightarrow \theta=\arcsin(0)=0,\\ u=\dfrac{1}{2}\Rightarrow \theta=\arcsin\left(\dfrac{1}{2}\right)=\dfrac{\pi}{6}} \\\\ &=& \dfrac{1}{3}\displaystyle \int \limits_{0}^{\dfrac{\pi}{6}} \dfrac{\cos(\theta)}{ \sqrt{1-\Big(\sin(\theta)\Big)^2} }\ d\theta \\\\ &=& \dfrac{1}{3}\displaystyle \int \limits_{0}^{\dfrac{\pi}{6}} \dfrac{\cos(\theta)}{ \cos(\theta) }\ d\theta \\\\ &=& \dfrac{1}{3}\displaystyle \int \limits_{0}^{\dfrac{\pi}{6}} d\theta \\\\ &=& \dfrac{1}{3} \Big[ \theta \Big]_{0}^{\frac{\pi}{6}} \\\\ &=& \dfrac{1}{3}\cdot \dfrac{\pi}{6} \\\\ &\mathbf{=}& \mathbf{\dfrac{\pi}{18}} \\ \hline \end{array}\)

I was trying to solve the following question:

\(\begin{array}{|rcll|} \hline x^2(x+3y)-y^3 &=& 3 \\ x^3 + 3x^2y-y^3 - 3 &=& 0 \\\\ \mathbf{f(x,y)} & \mathbf{=} & \mathbf{x^3 + 3x^2y-y^3 - 3} \\\\ \dfrac{\partial f} {\partial x} &=& 3x^2+6xy \\ \dfrac{\partial f} {\partial y} &=& 3x^2-3y^2 \\ && \boxed{\text{Formula: }\\ \dfrac{dy}{dx} = -\dfrac{\dfrac{\partial f} {\partial x}} {\dfrac{\partial f} {\partial y}} } \\ \dfrac{dy}{dx} &=& -\dfrac{ 3x^2+6xy } { 3x^2-3y^2 } \\\\ \dfrac{dy}{dx} &=& -\dfrac{ 3(x^2+2xy) } { 3(x^2-y^2) } \\\\ \dfrac{dy}{dx} &=& -\dfrac{ x^2+2xy } { x^2-y^2 } \\\\ \mathbf{ \dfrac{dy}{dx}} &\mathbf{=}& \mathbf{\dfrac{ x^2+2xy } { y^2-x^2 }} \\ \hline \end{array}\)

integrating w substitution

\(\large{\int \limits_{0}^{2} \dfrac{x}{ \sqrt{1+2x^2} }dx}\)

\(\begin{array}{|rcll|} \hline && \mathbf{\large{\int \limits_{x=0}^{x=2} \dfrac{x}{ \sqrt{1+2x^2} }dx}} \\ && \quad \boxed{ \text{substitute: } \\ u = 1+2x^2,\ du=4x\ dx,\\ x=0 \Rightarrow u=1+2\cdot 0^2=1,\\ x=2\Rightarrow u=1+2\cdot 2^2=9 } \\ &=& \int \limits_{u=1}^{u=9} \dfrac{x}{ \sqrt{u} }\dfrac{du}{4x} \\\\ &=& \dfrac{1}{4} \int \limits_{u=1}^{u=9} \dfrac{1}{ \sqrt{u} }du \\\\ &=& \dfrac{1}{4} \int \limits_{u=1}^{u=9} u^{-\frac{1}{2}} du \\\\ &=& \dfrac{1}{4} \left[ \dfrac{u^{\frac{1}{2}}}{\frac{1}{2}} \right]_{u=1}^{u=9} \\\\ &=& \dfrac{1}{4}\cdot \dfrac{2}{1} \left[ u^{\frac{1}{2}} \right]_{u=1}^{u=9} \\\\ &=& \dfrac{1}{2} \left( 9^{\frac{1}{2}}-1^{\frac{1}{2}} \right) \\\\ &=& \dfrac{1}{2} ( \sqrt{9} -1 ) \\\\ &=& \dfrac{1}{2} ( 3 -1 ) \\\\ &=& \dfrac{2}{2} \\\\ &\mathbf{=}& \mathbf{1} \\ \hline \end{array}\)

What is the sum of this sequence?
1000^2 + 999^2 - 998^2 - 997^2 +996^2 + 995^2 - .........+ 4^2 + 3^2 - 2^2 - 1^2.

\(\begin{array}{|rcll|} \hline && \mathbf{1000^2 + 999^2 - 998^2 - 997^2 +996^2 + 995^2 - \ldots + 4^2 + 3^2 - 2^2 - 1^2} \\ &=& \sum \limits_{k = 1}^{250} \Big( (4k)^2+ (4k-1)^2- (4k-2)^2 -(4k-3)^2 \Big) \\ &=& \sum \limits_{k = 1}^{250} \Big( 16k^2 +16k^2-8k+1-16k^2+16k-4 -16k^2+24k-9 \Big) \\ &=& \sum \limits_{k = 1}^{250} \Big( -8k+1 +16k-4 +24k-9 \Big) \\ &=& \sum \limits_{k = 1}^{250} \Big( 32k-12 \Big) \\ &=& \sum \limits_{k = 1}^{250}32k-\sum \limits_{k = 1}^{250}12 \\ &=& 32\sum \limits_{k = 1}^{250}k- 12\cdot 250 \\ &=& 32\left(\dfrac{1+250}{2}\right)\cdot 250- 12\cdot 250 \\ &=& 16\cdot 251 \cdot 250- 12\cdot 250 \\ &=& 250( 16\cdot 251 - 12) \\ &=& 250\cdot 4004 \\ &\mathbf{=}& \mathbf{1001000} \\ \hline \end{array}\)