Melody

I have now answered this question twice.

Your link does not work but I believe I found the question that you meant. 

The meaning of this question is unclear.

If Mickey was given 10 fewer matches does that mean that Minnie gets 10 more?

How is the box shared.  Are there any matches left in the box?

Unclear questions like this cannot be definitely answered.  I know it is not the fault of the students. 

Perhaps you should answer by explaining why the question is unclear and therefore unanswerable.

Try proofreading your question

Does this make sense to you?

"A circle is centered at  and has an area of 48pi. "

The magnitude of a point on the complex plane is just the distance of that point to the 0.   (the origin)

That is why the symbol used is the same as the absolute sign.

In your case  |w|=2   assuming that each of those arcs is 1 unit apart 

I would assume that that point is 

 \(2e^{(\frac{3\pi}{4}i)} \\= 2cis(\frac{3\pi}{4})\\= 2[cos(\frac{3\pi}{4})+isin(\frac{3\pi}{4})]\\ =2[-\frac{1}{\sqrt2}+i*\frac{1}{\sqrt2}]\\ =\sqrt2[-1+i]\\\)

what CPhill has written is also correct.

I'm finding the notation really confusing so I am going to change it

\(x=Z+\alpha \qquad \text{where } Z=\lfloor x \rfloor\;\; and \;\;\;0\le\alpha<1\)

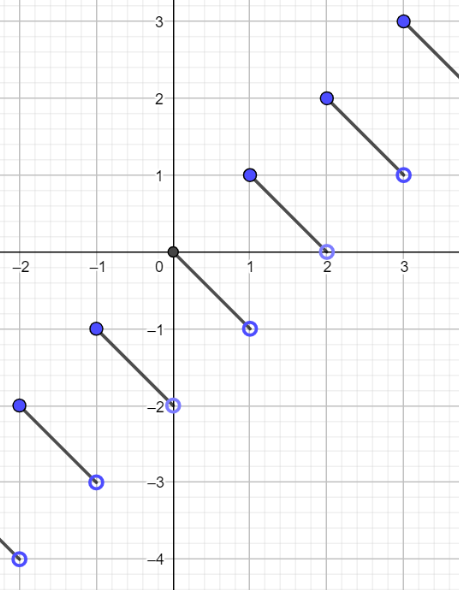
\(f(x)=f(Z+\alpha)=Z-\alpha\)

f(3.2)= 3-0.2=2.8

f(-3.2)=f(-4+0.8) =-4-0.8 = -4.8

So this function certainly isn't even of odd.

It is not continuous either.

The continuous segments are decreasing but I doubt that is valid, the graph as a whole is not decreasing.

anyway, that is something for you to think about.

Here is the graph

I do not know why it has not happened for me, maybe becasue I am a moderator.   

It happens automatically becasue balls is a slang term for testicals.

I did not get either of these answers.

\(ar^{22}=16\qquad and \qquad ar^{27}=24\\~\\ \frac{ar^{27}}{ar^{22}}=\frac{24}{16}\\ r^5=\frac{3}{2}\\~\\ r=\left( \frac{3}{2} \right)^{1/5} \\~\\ ar^{22}=16\\~\\ a=16*\left( \frac{2}{3} \right)^{22/5} \\~\\ g_{43}=ar^{42}\\~\\ g_{43}=16*\left( \frac{2}{3} \right)^{22/5} \left(\left( \frac{3}{2} \right)^{1/5}\right)^{42}\\~\\ \displaystyle g_{43}=\frac{2^4*2^{22/5}*3^{42/5}}{3^{22/5}*2^{42/5}}\\~\\ \displaystyle g_{43}=\frac{2^4*3^{20/5}}{2^{20/5}}\\~\\ \displaystyle g_{43}=\frac{2^4*3^{4}}{2^4}\\~\\ \displaystyle g_{43}=3^4\\~\\ \displaystyle g_{43}=81\\~\\ \)

LaTex

ar^{22}=16\qquad and \qquad ar^{27}=24\\~\\
\frac{ar^{27}}{ar^{22}}=\frac{24}{16}\\
r^5=\frac{3}{2}\\~\\
r=\left(  \frac{3}{2} \right)^{1/5} \\~\\
ar^{22}=16\\~\\
a=16*\left(  \frac{2}{3} \right)^{22/5} \\~\\
g_{43}=ar^{42}\\~\\
g_{43}=16*\left(  \frac{2}{3} \right)^{22/5} \left(\left(  \frac{3}{2} \right)^{1/5}\right)^{42}\\~\\

\displaystyle g_{43}=\frac{2^4*2^{22/5}*3^{42/5}}{3^{22/5}*2^{42/5}}\\~\\
\displaystyle g_{43}=\frac{2^4*3^{20/5}}{2^{20/5}}\\~\\
\displaystyle g_{43}=\frac{2^4*3^{4}}{2^4}\\~\\
\displaystyle g_{43}=3^4\\~\\
\displaystyle g_{43}=81\\~\\
 

Your question does not make sense.

If Mickey was given 10 fewer matches does that imply that Minnie got 10 more?

When they shared the box does that mean that every match was given to either Minnie or Mickey or could some have been left in the box?